Иллюстрация примеров решения задач математического программирования в системе РАНОК

Задача 1. Найти глобальные экстремумы функции на множестве решений системы

Решение

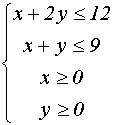
Задача 2. Найти глобальные экстремумы функции на множестве системы ограничений

Решение

Задача 3 (транспортная задача). Ежедневно в город поставляется одним видом транспорта 12 тонн картофеля из трёх колхозов: из первого колхоза по цене 4 рубля за тонну, из второго – по цене 3 рубля за тонну, из третьего – по цене 1 рубль за тонну. Чтобы поставка картофеля в город была произведена своевременно, необходимо на погрузку требуемых 12 тонн затратить не более 40 минут. Известно, что в первом колхозе уровень механизации позволяет погрузку 1 тонны производить за одну минуту, во втором – за 4 минуты, в третьем – за 3 минуты. Производственные мощности этих колхозов следующие: первый колхоз должен ежедневно выделять для поставки в город не более 10 тонн, второй – не более 8 тонн, третий – не более 6 тонн. Как распределить заказы на поставку12 тонн между колхозами, чтобы общая стоимость привозимого в город картофеля была минимальной?

Минимизировать целевую функцию

при условиях

Решение

Сходимость результатов решения данным способом обеспечивается увеличением глубины рекурсии при разбиении области определения функции. При этом, следует отметить ряд очевидных преимуществ перед многими существующими способами: применение -операций позволяет кусочно описывать области ограничений любой сложности, а применение образов-моделей в контексте системы РАНОК позволяет работать с любой размерностью пространства.