Применение интегральных преобразований для спектрального анализа диагностических сигналов

З.С. Волкова,

преп., volkovazs@rambler.ru,

А.А.Абу Газал,

асп., gazal.ayman@yandex.ru,

А.В. Лисенков,

инж., mangekusharingan@mail.ru,

НИЯУ МИФИ, г. Москва

Приведены результаты спектрального анализа диагностических сигналов, полученных методами функциональной электрофизической диагностики, при физико-механических испытаниях проводниковой меди на растяжение. Применяли методы дискретного преобразования Фурье, непрерывного вейвлетного преобразования и метод гармонического анализа. Особенности спектральных характеристик исследовали с помощью функций временных окон Ханна, Хемминга и Гаусса путем сдвига параметров окна относительно начала координат. Наибольшие искажения спектра диагностического сигнала наблюдали при использовании окна Ханна. Результаты спектрального анализа были смоделированы на макете виртуального прибора.

During physical and mechanical tests of copper wire tension, results of spectral analysis of diagnostic signals were obtained by functional diagnostics of electrophysical methods. Have been used the methods of Discrete Fourier transform, continuous Wavelet transform and Harmonic analysis method. Specific spectral characteristics were investigated using Hann, Hamming and Gaussian temporal windows functions, by shifting window parameters relative to the coordinate system origin. Maximum distortion spectrum of diagnostic signal was observed using Hann window. Results of spectral analysis were simulated on Scale model of the virtual device.

1. Анализ сигналов на основе непрерывного вейвлетного преобразования

Непрерывное вейвлет-преобразование есть интегральное преобразование, где под знаком интеграла стоит скалярное произведение функции диагностического сигнала и базисных функций вида

параметр b предназначен для сдвига функции по временной оси, а параметр а – для сдвига функции по оси частот. Непрерывное вейвлет-преобразование (НВП) представляли в виде:

Базисные функции называются вейвлетами. Они являются вещественными, определены на некотором интервале и рассматриваются как масштабированные функции для невозмущенной функции Большие значения параметра а соответствуют низким частотам, малые – высоким.

Обычно анализ диагностических сигналов необходимо выполнить как во временной, так и в частотной областях, при этом используются два подхода к их описанию: матричное описание, применяемое в линейной алгебре, и амплитудно-частотный анализ – в частотной области.

Вейвлет-анализ диагностируемых сигналов в среде MathCAD выполнен с помощью встроенных функций wave и iwave. Подробную расчетную методику обработки сигналов можно найти в работах [1,2]. Функция wave является прямым дискретным вейвлет-преобразованием. В качестве вейвлетообразующей функции используется вейвлет Добеши. Функция возвращает вектор вейвлет-коэффициентов, которые представляют собой прямоугольные гармоники. Чем выше уровень разложения, тем выше частота гармоник. Вейвлет-коэффициенты служат в дискретном преобразовании для масштабирования и локализации во времени вейвлет-функций, участвующих в разложении. Вейвлет-спектрограммы более информативны, чем Фурье-спектрограммы. При помощи вейвлет-фильтра можно выявить локальные особенности сигналов с привязкой их ко времени или пространственным координатам. Чем резче выражается «особенность» сигнала, тем сильнее она выделяется на спектрограмме и тем выше уровни вейвлет-коэффициентов. Вейвлет-спектрограммы отчетливо выделяют такие детали, как небольшие разрывы сигналов, изменение знака первой и второй производных, изменение числа гармоник во времени и др. Нами установлено, что при механических испытаниях вейвлет-фильтры эффективно выделяют из спектра гармоники, связанные с релаксацией упругих напряжений. В этом случае в детектированном сигнале появляются особые локальные составляющие. В спектре часто наблюдается последовательное появление «сдвоенных» импульсов, имеющих противоположные знаки с высокими значениями амплитуды.

Вейвлетное преобразование (функция iwave) дает полное восстановление исходного сигнала. При восстановлении сигнала можно применять фильтрацию, варьируя уровень детализации, что позволяет, например, исключать те же высокочастотные гармоники коэффициентов, выделяя отдельные фрагменты эксперимента.

2. Применение интегральных преобразований при исследовании физико-механических свойств сплавов

Использование интегральных преобразований при анализе диагностических сигналов начнем с рассмотрения совместных процедур ДПФ и НВП для результатов механических испытаний (рис.1-5). На макете виртуального прибора показан результат применения функций wave и iwave для временной зависимости диагностического сигнала, полученного при испытаниях на растяжение проводниковой медной проволоки (Æ 0,23 мм, l= 180 мм) при напряжении близком к пределу текучести (около 220 МПа). Процедура обработки диагностического сигнала заключалась в последовательном применении вейвлетного преобразования к временной зависимости функции , выделении шумов и полезной составляющей из сигнала. После указанной процедуры декомпозиции первоначальный сигнал был восстановлен с помощью функции iwave. Длительность диагностического сигнала во времени соответствовала времени проведения испытаний, т.е. составляла около десяти часов (рис.1).

Весь временной интервал испытаний был разбит на отдельные участки длительностью, равной одному часу. Для каждого такого участка на временной зависимости выделялся соответствующий временной интервал диагностического сигнала и проводился гармонический анализ. Число гармоник рассчитывалось по методике [3] и отображалось на экране виртуального прибора в виде ступенчатой функции (3, рис.1). Для участка этой функции, указанного на графике курсором, число гармоник равно N=794.

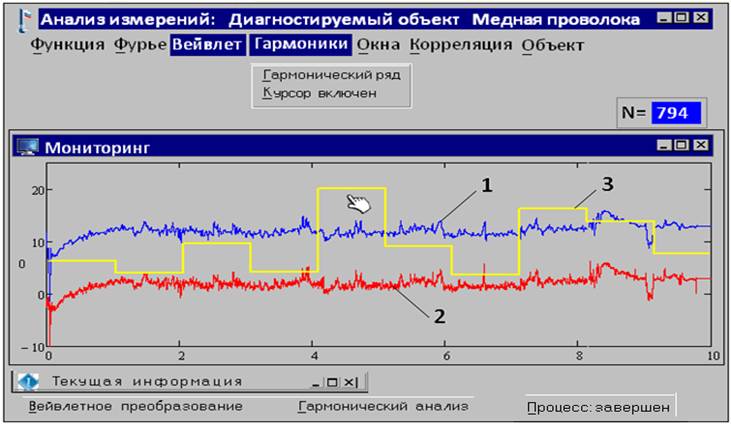
Рис. 1. Показан очищенный с помощью функции wave сигнал (1), восстановленный исходный сигнал с помощью функции iwave (2) и временная зависимость числа гармоник N тригонометрического ряда Фурье (3). Текущее значение числа гармоник на указанном курсором участке равно N=794. Амплитуда сигналов 1 и 2 показана в мкВ, время – в часах. Сигналы 1 и 2 сдвинуты по оси «y» друг относительно друга на десять единиц

Амплитудно-частотные характеристики диагностического сигнала, рассчитанные с помощью выражения (2) показаны на рисунке 2 (для n = k =100). Верхний график соответствует ДПФ для неочищенного сигнала, где вместе с информативной компонентой (трендом) присутствует шумовая составляющая. Нижний график построен для функции, которая предварительно обработана с помощью вейвлет-фильтра. При обработке использовались высокие значения коэффициентов разложения. Шумовая компонента была удалена алгебраическим вычитанием из экспериментальной зависимости функции, полученной после прохождения вейвлет-фильтра. Из представленного графика видно, что информативная составляющая сигнала имеет четко выраженный низкочастотный характер.

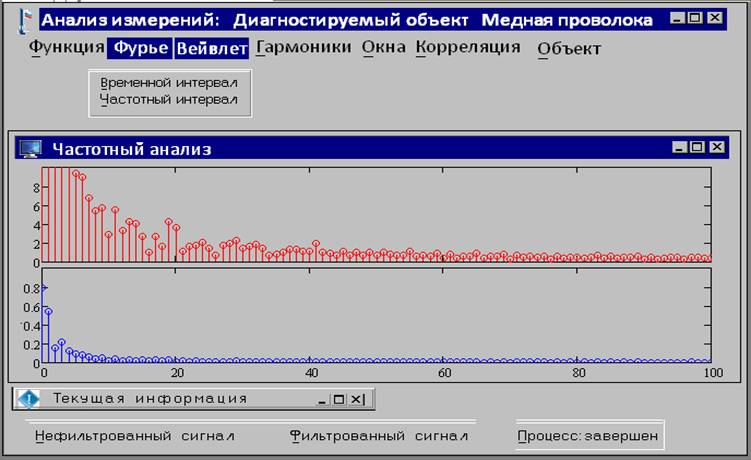
Рис. 2. Результаты применения ДПФ к экспериментальной временной зависимости диагностического сигнала (верхний рисунок) и к временной зависимости диагностического сигнала, предварительно очищенного с помощью вейвлет-фильтра – нижний рисунок

Временные окна позволяют изучать особенности спектральных характеристик путем сдвига параметров окна относительно начала координат. Наибольшие искажения спектра получаются при использовании окна Ханна (верхний график, рис.3). На этом рисунке показаны спектры для неочищенного сигнала. Результат применения окна Хемминга (средний график, для n = k = 500) похож на результат ДПФ для неочищенного сигнала (рис.2). Использование окна Гаусса предоставляет возможность перехода к частотно-временному представлению, поскольку в функции содержится множитель, зависящий от времени.

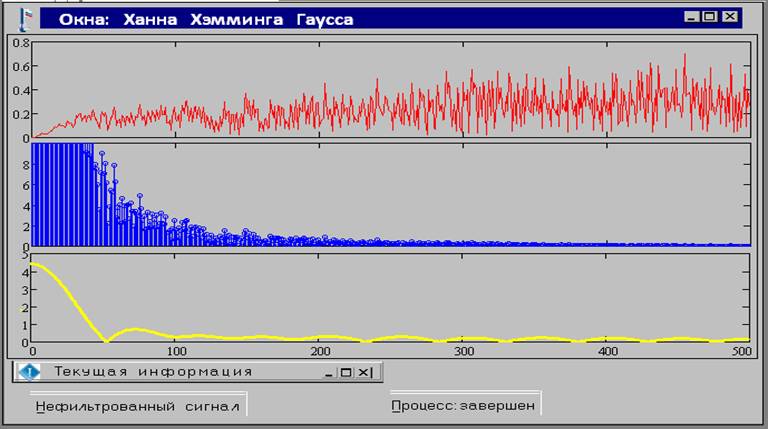
Рис. 3. Результаты применения ДПФ к экспериментальной временной зависимости диагностического сигнала с использованием временных окон Ханна, Хемминга и Гаусса (сверху вниз)

Сравнительные результаты применения временных окон к сигналу, преобразованному с помощью вейвлет-фильтра, показаны на рисунке 4. Можно видеть, что для всех трех окон результаты заметно отличаются от рисунка 3: для окна Ханна наблюдается два «последовательно соединенных» участка спектра около значения k~250. Для этих значений k один из коэффициентов вейвлет-разложения (коэффициент восьмого уровня) показывает наличие ступеньки на соответствующей диаграмме НВП.

Рис. 4. Результаты применения ДПФ к экспериментальной временной зависимости диагностического сигнала с использованием временных окон Ханна, Хемминга и Гаусса (сверху вниз) к временной зависимости диагностического сигнала, предварительно очищенного с помощью вейвлет-фильтра

Также заметно сокращается эффект частокола для окна Хемминга (на средней части рисунка), а кривая для окна Гаусса «приподнимается» над осью х в начале координат.

Литература

1. Дьяконов В.П. Вейвлеты. От теории к практике. М.: СОЛОН-Пресс, 2004.

2. Кирьянов Д.В. Mathcad 12. СПб.: БХВ-Петербург, 2005.

3. Сурин В.И., Евстюхин Н.А., Шубняков А.В. Гармонический анализ формы электрических сигналов, возникающих при ползучести металлов и сплавов.// Сб.научных трудов. Научная сессия МИФИ-2004. М.: МИФИ, 2004, т.9,с.121–122.