Универсальный алгоритм размещения связных объектов

в двухмерном пространстве

Е.В. Тишкевич,

асп. МТУСИ. г. Москва,

Е.И. Артамонов,

зав. лаб.,  д.т.н., проф.,

ИПУ РАН, г. Москва

Введение

Задача оптимального размещения системы взаимосвязных объектов в некоторой ограниченной области пространства (в монтажном пространстве) при выполнении требований высокой плотности размещения с минимизацией некоторой функции качества и выполнением целого ряда других технических ограничений встречается в проектировании достаточно часто. К таким задачам можно отнести планирование площадей застроек производственного предприятия, размещение в цеху станочного оборудования, размещение оборудования в корпусе самолета, размещение радиокомпонентов на плате и т.п.

Задача размещения

В случае проектирования радиоэлектронных устройств размещению предшествует компоновка, а результаты размещения используются при построении оптимальных соединений компонентов и получении графической документации.

В машинном проектировании наиболее разработанными являются методы размещения одногабаритных объектов, когда решение задачи сводится к определению суммарных длин связей каждого неразмещенного объекта с уже размещенными. Под связью при этом понимается периметр прямоугольника, ограничивающего связь, или величина, равная площади этого прямоугольника, или длина связи по алгоритму Прима в той или иной метрике и т.д. При этом можно однозначно определить одну из заранее назначенных позиций для размещения объекта.

Ниже описывается алгоритм, универсальность которого заключается в возможности получать различные варианты размещения, оптимальные в некотором смысле, как одногабаритных, так и разногабаритных объектов с коэффициентом заполнения поля, близким к единице.

Отсутствие необходимости в начальном размещении, простота реализации, универсальность, декомпозиционный подход, снимающий практически ограничения на размерность задач размещения, возможность сопряжения с программой трассировки следует отнести к основным достоинствам описываемого ниже алгоритма размещения.

Идея алгоритма группировки заключается в следующем. Пусть задано множество взаимосвязанных объектов . Каждому объекту mJ соответствует вектор описания , а множеству М – множество векторов описания .

Задача заключается в разбиении М по множеству X на m групп так, чтобы каждый объект mi принадлежал одной и толькой одной группе и чтобы объекты, принадлежащие одной группе, были "близкими", а объекты, принадлежащие разным группам, "неблизкими" в некотором смысле.

Для решения этой задачи необходимо количественно определить понятие "близости". В некоторых случаях число групп m можно выбрать априорно, но в общем случае этот параметр должен быть определен в процессе решения оптимизационной задачи. Пусть вектор описания содержит одну измеряемую характеристику и известна матрица А, опреде­ляющая связность элементов. Коэффициент "близости" mi объекта со всеми объектами, входящими в J группу, определим как отношение:

,

где                      nJ – число элементов, входящих в группу;

 – сумма числа связей mi элемента с nJ объектами, входящими в группу;

                   T – эвристическая константа                       

Объект входит в группу, если величина  не превосходит некоторого порогового значения εJ  для J группы. Сложность каждой группы ограничена сверху количеством входящих в нее объектов.

Минимизация функции качества позволяет определить оптимальное значение m.

,

где                      – число межгрупповых связей J группы;

 – число внутригрупповых связей при разбиении множества объектов на m групп.

Величина

является мерой близости между I и J группами,

где nI и nJ – число элементов в I и J группах соответственно;

SIJ - межгрупповые связи между ними.

Каждая группа может рассматриваться как новый объект. На мон­тажном поле размещают вначале группы объектов, а затем объекты внутри групп. Такая схема позволяет сохранить универсальность парал­лельных алгоритмов размещения, в то же время увеличивается быстродей­ствие за счет уменьшения размерности частичных задач.

В алгоритме рассматриваются две постановки задачи размещения: размещение объектов на монтажном поле, когда коэффициент заполнения η ≤ 0,6; размещение объектов на монтажном поле, когда коэффициент заполнения η > 0,6.

В свою очередь задача размещения в первой постановке подразде­ляется на два варианта: размещение объектов с различными линейными размерами, когда интервал разбиения на несколько порядков меньше размеров элементов и по сути решается непрерывная задача; размещение объектов, когда дискрет таков, что число узлов сетки, в которые по­мещаются характерные точки элементов, сравнимо с числом элементов. В этом случае задается также описание монтажного поля множеством координат позиций, в которые размещаются объекты. Эта версия исполь­зуется также для размещения одногабаритных объектов.

Для обеих постановок можно сформулировать две задачи.

Задача поместимости. В данной области найти хотя бы один ва­риант размещения объектов без пересечения при η < 1.

Задача конструирования. Из всех вариантов размещения выбрать хотя бы один, удовлетворяющий всем заданным ограничениям (теплофизической совместимости, минимума суммарной длины связей, формы и др.).

В качестве проекций объектов на монтажную плоскость обычно бе­рутся геометрические фигуры, допускающие простое аналитическое опи­сание своих оболочек. Оболочку объекта можно рассматривать в каче­стве его геометрической модели, что дает возможность учитывать па­раметры объекта, не связанные с его конфигурацией. Для упрощения описания оболочек можно положить, что зоной влияния является описан­ный параллелепипед с основаниями, параллельными монтажному полю. Для двухмерного случая рассматриваются проекции зоны влияния на монтажную плоскость. Принятое допущение сильно упрощает задачу и алгоритм ее решения. Характер задачи плотного размещения требует перевода всех размеров объектов, монтажного поля, запрещенных зон в дискретные, что осуществляется программно. Это позволяет исключить иррациональ­ность в размерах объектов и обеспечить хорошее сопряжение их оболо­чек.

Для задачи размещения в первой постановке число объектов в группе ограничено сверху выбранным методом оптимизации функции ка­чества. Задача нахождения глобального экстремума функций многих пе­ременных не решена в общем виде в том смысле, что не существует еди­ного алгоритма, с помощью которого можно решить любую такую задачу.

Метод С.А. Пиявского (Институт кибернетики АН УССР) отвечает, как показало практическое использование предлагаемой методики, сформулированным выше требованиям. Предлагаемая эвристическая проце­дура приводит к удовлетворительному решению поставленной задачи, что, конечно, не означает, что решение является строго оптимальным в каком-то смысле.

Качество размещения объектов внутри группы оценивается по сум­марной длине связей L с ограничением по длине наибольшей связи.

,

где       aij – число связей i и j объектов из kj, назначенных в группу.

Пространство поиска имеет размерность 2Кi. Точкам этого про­странства соответствуют всевозможные размещения ki элементов груп­пы на монтажной плоскости. Экстремум функции качества ищется в 2Кi -мерном параллелепипеде.

                                    

где       i – 1, 2, … , ki,.

Алгоритм поиска экстремума базируется на двух основных идеях, первая из которых принадлежит С.А. Пиявскому, вторая – Бруксу (Вели­кобритания) .

Алгоритм поиска в общих чертах состоит в следующем:

1) с помощью датчика случайных чисел с равномерным распределе­нием в 2Ki-мерном параллелепипеде формируются последовательные случайные точки, в которых вычисляется значение критерия качества;

2) по каждой паре точек с учетом вычисленного в них критерия качества вычисляется радиус шара R в пространстве поиска с центром в точке с "худшим" значением критерия качества, а параметры "лучшей" точки заполняются.

,

где                С – константа Липшица.

В дальнейшем критерий качества вычисляется лишь в тех случайных точках, которые попадают в дополнение к объединению совокупности этих шаров. Тем самым в процессе поиска исходный параллелепипед по­крывается все большим числом шаровых областей до тех пор, пока 2Кi -мерный объем дополнения не окажется меньше заданного числа (число δ – заданная точность по аргументу);

3) мера дополнения оценивается по методу Монте-Карло;

4) константа Липшица С критерия качества оценивается методом до­верительных интервалов по некоторым предварительно вычисленным зна­чениям критерия качества в некотором числе случайных точек. Эти зна­чения в последующем используются так, как описано в пункте 2. Кон­станта Липшица в процессе поиска уточняется;

5) после того, как мера дополнения к шаровым областям станет меньше заданного числа, исходная область поиска "поджимается", т.е. заменяется пересечением исходного параллелепипеда с новым, у которо­го стороны в Q раз меньше (Q – эвристическая константа) и центр ко­торого находится в "лучшей" точке предыдущего этапа поиска;

6) поиск в новой области ведется так же, как и в предыдущей, и вся изложенная выше процедура повторяется циклически до тех пор, по­ка "лучшие" значения критерия качества на двух последовательных эта­пах не станут отличаться меньше, чем на ε (ε > 0 есть точность вычисления экстремума).

Для формирования точки в пространстве поиска определяются ориен­тация каждого объекта из выбранной группы и его положение на плоскос­ти. Для определения ориентации происходит обращение к датчику случайных чисел с равномерным распределением на отрезке (0,1). Если , то max (аi, bi) параллельна оси X. Если , то max (аi, bi) параллельна оси Y (ξ – случай­ная величина отрезка (0,1)).

По ориентации элемента определяется допустимая зона координат на монтажной плоскости (условие поместимости). Если признак ориен­тации I, то зона координат для элемента из группы имеет размеры:

;                   .

В зону координат случайно выбрасывается точка и производится линейное преобразование:

;                            ,

где                Ai0, Bi0 – координаты нижней левой вершины рабочей зоны для i элемента;

                xi, yi – координаты центра этого элемента.

По размерам элемента и координатам его центра определяются коорди­наты вершин, и они запоминаются. Те же операции выполняются для (i + I)-го элемента.

Далее определяются пересечения (i + I)-го элемента с предше­ствующими i элементами.

Пересечение двух прямоугольников с параллельными сторонами – прямоугольник. Пусть координаты вершин прямоугольников:

Признаком непустого пересечения двух прямоугольников является выполнение неравенств:

                и                    

Если пересечение пусто, то определяются ориентация и коорди­наты следующего элемента, если непусто, то ориентация и координаты (i + I)-го элемента определяются заново. Процедура повторяется, по­ка не будут исчерпаны все элементы размещаемой группы. Размещение без пересечения фиксируется. Фиксированное размещение есть 2Ki-мер­ная точка для вычисления функции качества.

При размещении объектов, когда дискрет таков, что число узлов сетки, в которые помещаются центры элементов, сравнимо с числом эле­ментов, все процедуры сохраняются, но так как вероятность случайного выброса незанятой ячейки уменьшается с увеличением числа размещенных элементов, производится случайный выбор ячейки только из числа неза­нятых ячеек, а занятые ячейки запоминаются.

Пусть ячейки и ряда пронумерованы, как показано на рис. 1. Чис­ло ячеек будет равно:                    ,

где                q – рядность по вертикали;      p – по горизонтали.

Случайным образом выбирается номер ячейки:               

где i возрастает, принимая последовательно значения i = 1, 2, ... , n.

Тогда номер ряда по вертикали равен:                         ,

Номер ряда по горизонтали:                                                      .

Тогда координаты элемента будут:                                       ;                   ,

где                a0 , b0 – координаты первой ячейки; t1  t2 – соответственно шаг по горизонтали и шаг по вертикали.

Если I1 = 0, то присваивается значение I1 = q.

 

 

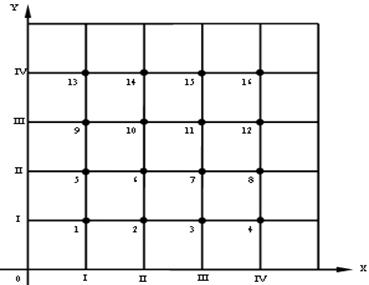
рис. 1. Расположение ячеек на монтажном поле

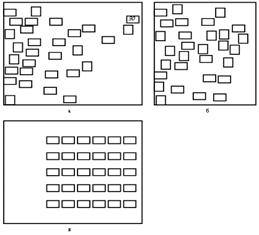
рис. 2. Примеры решения задачи размещения в различных постановках: 

а – размещение 30 объектов с фиксированным объектом № 30; б – размещение без фиксации объекта № 30;  в – размещение тех же одногабаритных объек­тов на заранее указанные позиции с фиксированной ориен­тацией

На рис. 2 и рис. 3 приведены примеры реализации алгоритма. На рис. 2,а демонстрируется чувствительность алгоритма к связности объектов. Коэффициент заполнения выбран специально небольшим.

 

                                                            

 

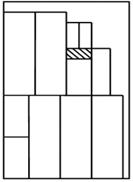
                                                                                  а                                                                                           б

                рис. 3. Примеры размещения элементов:  а – плотное размещение 11 элементов;  б – размещение 107 разногабаритных объектов

Объект № 30 фиксирован в правом верхнем углу монтажного поля, и все объекты, связанные с ним, вытягиваются в цепочку от объекта № 30 к остальной группе. На рис. 2,б показано размещение объектов для той же задачи без фиксации элемента № 30.

На рис. 3,б приводится размещение 107 элементов с коэффициен­том заполнения η = 0,55.

При размещении объектов на монтажном поле, когда коэффициент заполнения η > 0,6 в соответствии с принятым допущением о прямоугольности конфигурации оболочек объектов, строится убывающая и од­нозначная ступенчатая функция, начиная с левого нижнего угла поля.

Пусть размещены i объектов, тогда (i + I) объект размещается поочередно на каждую иступеньку". Критерий качества считается только для положений объекта, которые не нарушают признака убывания сту­пенчатой функции и ее однозначности (рис. 4).

При этом в качестве окончательного его размещения выбирается положение с минимальным значением критерия качества.

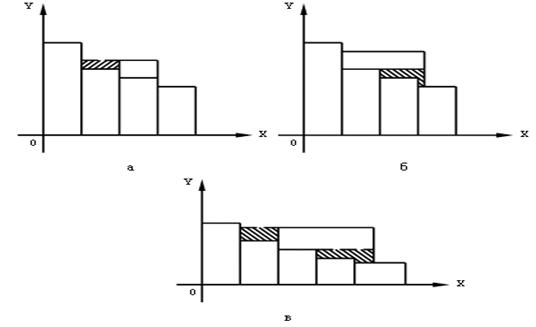
рис. 4. Построение ступенчатой функции:

а – нарушение условий убывания; б – нарушение условия однознач­ности; в – нарушение условия убывания и однозначности

 

Пусть построена ступенчатая функция для i объектов.

      ,при             

где                i – номер объекта;

                        k – номер ступеньки   y   i-й функции   xi.

Пусть далее k0 есть та ступенька размещения, на которой (i + I) объект не приводит к нарушению признаков убывания и однозначности функции, и, кроме того, эта позиция доставляет минимум критерию ка­чества.

Тогда                xi+1 = xi ,      при               k ≠ k0 ,         ,            , , при ,

                             ,            ,                                         при               ,

где         и  - номера двух новых ступенек, полученных из одной старой с номером k0,

.

На самом деле теперь                      , , и для всех номеров  нужна перенумерация. При построении функции  необходимо увеличить номера ступенек, начиная с  на единицу ( и т.д.).

Итак:

                                                               при               ;

                                             при               ;

                                                               при               ;

                                                         при               .

Если для (i + I) объекта все позиции оказались запретными, т.е. куда бы он ни стал, нарушается либо однозначность, либо убываемость ступенчатой функции, то критерий качества с некоторым весовым коэф­фициентом учитывает площадь полости, которая получается, если продол­жить стороны этого объекта влево и вниз до пересечения с "лестницей". И так же, как и в первом случае, фиксируется размещение с минималь-i ным значением критерия качества. Образовавшаяся полость "закрывает­ся" для размещения последующих k элементов, если она не может быть использована, так что ступенчатая функция по-прежнему остается одно­значной и убывающей.

Площадь полости, возникающая из-за нарушения однозначности или убывания ступенчатой функции, считается следующим образом:

,

где                S1 – полость из-за неубывания;

      S2 – полость из-за неоднозначности.

,

где                kh – номер ступеньки, с которой .

,

где                kh – номер последней ступеньки, над которой нависает (i + I)-й элемент.

 

Программа по алгоритму содержит около 900 операторов и работает в составе автоматизированной системы проектирования "Графика", разработанной в Институте проблем уп­равления Российской Академии Наук.