Методика исследования динамического объекта с ограничениями
по выходной координате на основе метода
инвариантного погружения
В.М. Понятский,
нач.
сектора, к.т.н, доц.,
ГУП «КБП», е-mail: kbkedr@tula.net, г.Тула
Важной
задачей при исследовании объекта управления является оценка его характеристик
по результатам измерений информационных сигналов. При натурных испытаниях
получают сигналы с объекта управления, функционирующего в условиях пассивного
или активного эксперимента. Анализ качества работы объекта управления по результатам
его испытаний проводится на основании измеренных информационных сигналов. Эти
сигналы обладают рядом особенностей (зашумленность сигналов, нестационарность
сигналов), которые необходимо учитывать при идентификации объекта управления.
Нелинейный
объект с линейным наблюдателем может быть описан следующей системой нелинейных
дифференциальных уравнений [1-3]:
; (1)
,
где 
- вектор управления; 
- вектор наблюдения; 
- расширенный вектор
состояния, включающий параметры объекта; 
- вектор формирующих
шумов интенсивностью 
; 
- вектор шумов
измерения интенсивностью 
; 
- функция состояния; 
- матрица коэффициентов; 
- матрица наблюдения.
Непрерывный
алгоритм инвариантного погружения для нелинейного объекта с линейным наблюдателем
(1) имеет вид [1-3]:
(2)
где 
- оценка расширенного вектора состояний; 
- корреляционная матрица ошибок фильтрации; начальные условия:
; 
Необходимо по измеряемым входным сигналам (вектор управления U) и выходным сигналам (вектор наблюдения z), при известной структуре объекта (матрицы f, G) и измерителя (матрица
наблюдения H) получить оценку элементов
матриц f, G.
Рассмотрим
процесс конструирования непрерывного алгоритма идентификации динамического
объекта на основе метода инвариантного погружения.
Разработка
алгоритма оценки коэффициента и постоянной времени нестационарного динамического
объекта при наличии ограничений по выходной координате.
Зададим
переменные расширенного вектора состояний следующим образом:
.
где 
- выходная координата; 
- коэффициент
передачи, 
; 
- постоянная времени.
Применительно
к алгоритму инвариантного погружения (2) имеем:
; 
; 
; 
.
В
случае наличия ограничений по выходной координате (рисунок 1) для вектора
наблюдений можно записать следующее выражение[4]:
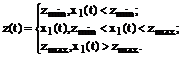
рис.
1 Схема динамического объекта с
ограничениями по выходной координате
Тогда
алгоритм оценки коэффициента передачи и постоянной времени при наличии ограничений
в выходной координате будет иметь следующий вид:
(3)
где 
– оценка выходной
координаты.
Уравнения
для дисперсии ошибки в этом случае имеют вид:
где 
Разработка алгоритма оценки коэффициента передачи, постоянной
времени и декремента затухания нестационарного динамического объекта при наличии ограничений по
выходной координате.
Зададим расширенный вектор состояний в виде:
,
где 
- выходная координата; 
- скорость изменения выходной координаты; 
- коэффициент
передачи, 
; - постоянная времени; 
; 
- декремент затухания.
Задание
и 
целесообразно при
величинах и значительно меньших
единицы и позволяет обеспечить лучшую сходимость к искомым коэффициентам
модели. Алгоритмы оценивания для случаев задания 
и 
приведены в работе [3].
Запишем
систему уравнений объекта:
Непрерывный
алгоритм оценивания для случая ограничений по выходной координате имеет вид в
соответствии с (2):
(4)
Проведено
тестирование разработанного алгоритма оценки коэффициента передачи и постоянной
времени для случая наличия ограничений в выходном сигнале: 
. При этом были заданы входной сигнал 
, коэффициент передачи K= 2 и постоянная времени T = 0.05.
При СКО формирующего шума 
и СКО шума в
измерениях 
На рисунке 2 приведены входной и выходной сигналы.
Результаты оценки коэффициента передачи и постоянной времени с учетом ограничений
в выходном сигнале и без учета ограничений изображены на рисунке 3. Полученная
оценка коэффициента передачи с использованием алгоритма без учета ограничений
имеет заниженные результаты (до 50 %), а полученные оценки постоянной времени с
учетом и без учета ограничений близки.
рис.
2 Входной и выходной сигналы динамической
системы
рис.
3 Оценки коэффициента передачи
На
рисунках 4 - 5 приведены исходные сигналы и результаты оценки коэффициента
передачи 
сервопривода беспилотного
вращающегося по крену летательного аппарата. В качестве исходных данных
использована телеметрическая информация, полученная с борта летательного
аппарата в ходе натурных испытаний: сигнал с входа сервопривода и сигнал с
выхода датчика углового положения рулей. Несмотря на то, что сервопривод, как
правило, представляет собой сложную динамическую систему, оценка его влияния на
качество функционирования системы управления может быть осуществлена по
изменению первой гармоники полезного сигнала в полосе рабочих частот системы.
Поэтому оперативный анализ влияния сервопривода на качество управления
летательным аппаратом может быть осуществлен через оценку его коэффициента передачи
и постоянной времени. На рисунке 3 приведены результаты оценки коэффициента передачи
сервопривода с использованием алгоритмов, спроектированных на основе метода инвариантного погружения. Оценка
проводилась при следующих параметрах алгоритмов: 
; 
; 
; 
градусов; 
градус/В; 
1/с; 
градусов; 
градусов. Для сравнения приведены результаты оценки
коэффициента передачи сервопривода без учета ограничений по выходной координате.
Учет ограничений по выходной координате обеспечивает более точную оценку
коэффициента передачи сервопривода [5].
рис.
4 Исходные сигналы: u - с
входа рулевого привода, z - с выхода сервопривода
рис. 5 Результаты оценки коэффициента передачи сервопривода:
- без учета ограничений по выходной координате;
- с учетом ограничений по выходной координате
Использование
по предложенной методики на основе метода инвариантного погружения обеспечивает
оценку характеристик динамического объекта по экспериментальным данным при наличии
ограничений по выходной координате.
Литература
1.
Сейдж Э.П., Мелса Дж.Л. Идентификация систем управления. – М.: Наука. -
1974.
2. Ponyatsky V.M., Nadezhdin Е.N. Neural networks for
parameter identification of servo-drives of the flying device //9 th IFAC
Workshop “Adaptftion and Learning in Control and Signal Processing”
ALCOSP’2007. Abstracts- //
3.
4.
Пальтов И.П. Нелинейные методы исследования автоматических систем. –
Москва: Энергия, 1960.-792с.
5.