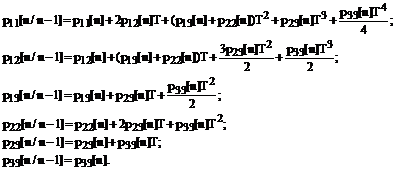Методика проектирования адаптивной
системы управления
с фильтром Калмана
В.М. Понятский,
нач. сектора, к.т.н, доц.,
ГУП «КБП», е-mail: kbkedr@tula.net, г.Тула
В системах управления повышение помехоустойчивости к воздействию
помех измерения координат объекта управления возможно обеспечить с помощью
фильтрации Калмана (рисунок 1) [1 -3].
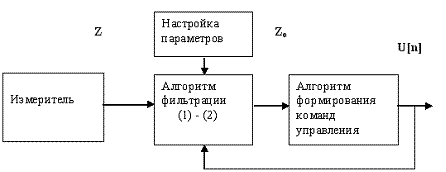
рис.
1 Структурная схема алгоритма формирования команд управления
Для
сглаживания наблюдений используется фильтр Калмана:
(1)
, (2)
где 
– вектор оценок
состояния объекта управления; 
– вектор состояния
объекта управления: 
; 
– переходная матрица; 
– вектор-столбец
наблюдений: 
; 
– матрица наблюдения; 
– корреляционная
матрица ошибок фильтрации; 
– вектор-столбец
гауссовских белых шумов наблюдения; 
– вектор-столбец
гауссовских формирующих шумов; 
– матрица интенсивностей
шумов наблюдений; 
– матрица интенсивностей
полезного сигнала; 
– матрица
коэффициентов; 
- вектор управления; 
- матрица коэффициентов
управления; 
- признак типа
измерителя или отсутствия измерений 
.
Дискретный
алгоритм оценивания состояния объекта управления в рамках методов фильтрации
Калмана имеет вид [1]:
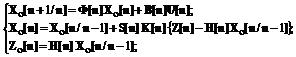(3)
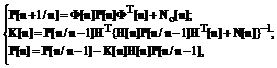(4)
где 
– вектор наблюдений; 
– вектор оценок наблюдений; 
- оценка вектора
состояния объекта управления; 
- оценка вектора
прогнозирования состояния объекта управления; 
- переходная матрица; 
- матрица наблюдения; 
- матрица
коэффициентов; 
– дисперсионная матрица вектора состояния объекта; 
- дисперсионная матрица оценки вектора состояния объекта; - вектор управления; - матрица коэффициентов управления; 
- признак типа
измерителя или отсутствия измерений 
.
Повышение
помехоустойчивости к воздействию нестационарных возмущений в виде помех
измерения состояния объекта управления и их возможным кратковременным
прерываниям при управлении обеспечивается взаимосвязанным выбором параметров алгоритма
фильтрации и алгоритма формирования команд управления (рисунок 1) [6].
Для
обеспечения устойчивости системы управления с фильтром Калмана вводится
обратная связь по командам управления u(t), исходя из выполнения
условия:
,
где 
- желаемая
передаточная функция замкнутой системы с фильтром; 
– передаточная функция
фильтра; 
- передаточная
функция системы без фильтра.
Формирование
требуемых динамических характеристик системы управления (полосы пропускания,
запасов устойчивости, точности и т.д.) может быть проведено методом частотных
характеристик и возможно при разных соотношениях полосы пропускания
системы без фильтра 
и полосы пропускания
фильтра 
. Если требуемое качество управления обеспечивается выбором
полосы пропускания системы без фильтра меньшей, чем полоса пропускания
фильтра :
то динамические свойства системы управления в
значительной степени определяются алгоритмом формирования команд управления, а
алгоритм фильтрации обеспечивает необходимое подавление в сигнале ошибки
управления помех измерения.
Требуемые
свойства системы при задании полосы системы без фильтра большей, чем полоса
пропускания фильтра :
обеспечиваются за счет повышения коэффициента
передачи системы (добротности) и уменьшения полосы пропускания фильтра. В этом
случае можно обеспечить полосу пропускания фильтра, соизмеримую с рабочей
полосой системы. Если обеспечить значительное повышение добротности при
понижении частоты пропускания фильтра, то система будет обладать высокими динамическими
свойствами, но при этом возрастает уровень шумовой составляющей в командах управления.
Традиционно
проектирование фильтра Калмана (1), (2) или (3), (4) осуществляется исходя из
априорной информации об интенсивностях полезного сигнала и шумов измерения. Реальные характеристики полезного сигнала и помех
измерения могут не соответствовать априорной информации в фильтре. Возможность
использования известных способов адаптации фильтра Калмана требует решения
задачи обеспечения выполнения требований к качеству управления. Для решения
этой задачи необходимо в соответствии с реальной обстановкой изменять не только
характеристики фильтра, но и производить соответствующую корректировку закона
управления, обеспечивая требуемое качество управления.
Используем достаточные статистики для обнаружения изменений в наблюдениях [1]:
(5).
Рассмотрим
проектирование фильтра Калмана для системы управления летательным аппаратом.
Синтез алгоритма фильтрации проведен исходя из гипотезы задания движения
объекта в виде уравнения 
, где 
- случайный белый шум
интенсивностью 
. В процессе движения объекта определяются ошибки управления
в условиях воздействия шумов измерения интенсивностью 
. Уравнения фильтра (1) и (2) в этом случае запишутся:
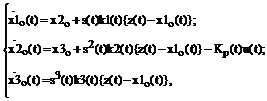
где
– ошибка управления, 
– команды управления с
выхода корректирующего фильтра; 
- коэффициент передачи;
- признак типа
измерителя, при отсутствии измерений: 
; 
, 
, 
- коэффициенты
фильтра.
Из
(2) следует, что для расчета
коэффициентов фильтра требуется решать матричное уравнение Риккати для , т.е. систему нелинейных дифференциальных уравнений. Для
упрощения вычислений будем рассчитывать коэффициенты для установившегося
случая, при 
, откуда 
, 
, 
. Коэффициенты фильтра имеют вид: 
, 
, 
, 
.
Кроме
сглаживания измеряемых координат объекта управления осуществляется также оценка
переменных состояния движения объекта. Передаточные функции фильтра Калмана по
переменным состояния имеют вид:
Произведение
коэффициентов 
определяет полосу
пропускания фильтра Калмана, и его эквивалентная постоянная времени может быть
определена: 
. То есть, чем больше отношение интенсивности No
полезного сигнала к интенсивности N шума измерения, тем шире полоса
пропускания фильтра Калмана. И наоборот, чем меньше отношение интенсивности No полезного
сигнала к интенсивности N шума измерения, тем уже
полоса пропускания фильтра Калмана и обеспечивается более эффективное
подавление помех измерения. Изменение полосы фильтра может быть осуществлено
выбором отношения интенсивностей полезного сигнала к шуму измерения, а также
заданием величины 
. Коэффициенты 
и 
в фильтре Калмана
определяют в полосе пропускания полезного сигнала величину фазового запаздывания.
Дискретный
алгоритм фильтрации для цифровой реализации получен на основании зависимостей
(3)-(4).
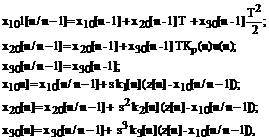
где 
– измеренные координаты
объекта управления; 
,
,
– оценки переменных состояния
объекта управления; 
- признак типа
измерителя, при отсутствии измерений: 
; Т – период дискретизации сигнала; 
,
,
- коэффициенты фильтра (4):
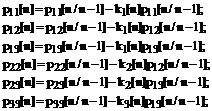
Выбор
полосы пропускания фильтра Калмана может быть проведен методом частотных характеристик.
Корректирующий фильтр обеспечивает требуемую устойчивость и точность системы
управления в условиях отсутствия
помех наблюдения
На
участке управления, где влияние помех измерения мало, полоса пропускания
системы без фильтра выбирается больше, чем
полоса пропускания фильтра : 
. Это позволяет обеспечить высокий коэффициент передачи
системы управления. Расширение полосы системы управления при увеличении
коэффициента передачи компенсируется уменьшением полосы пропускания фильтра.
На
этапе управления, где возрастает влияние помех, целесообразно полосу
пропускания системы без фильтра задавать меньше, чем
полоса пропускания фильтра : 
. В этом случае динамические свойства системы управления в
значительной степени определяются корректирующим фильтром, а фильтр обеспечивает
необходимое подавление помех измерения. Изменение полосы пропускания фильтра
обеспечивается в зависимости от типа измерительного устройства путем задания
соответствующего соотношения интенсивности полезного сигнала к интенсивности помех
измерения.
Сформированная
таким образом система имеет программно изменяющиеся параметры фильтра и блока
управления. Как правило, характер этих законов выбирается исходя из худшей
помеховой ситуации, что приводит к занижению динамических характеристик
системы. Однако, при отработке управляющих воздействий возможно появление в
ошибке управления динамической составляющей.
Обеспечим
в сформированной системе управления её адаптацию к появлению в ошибке
управления динамической составляющей. Для обнаружения динамической составляющей
в ошибке управления на фоне помех зададим выражения для отношения правдоподобия
при гипотезах [3]:
- в ошибке управления отсутствует динамическая составляющая;
- в ошибке управления
имеется динамическая составляющая.
Для
достаточной статистики получаем (5) [1]:
.
Правила
выбора решения, основывающиеся на отношении правдоподобия, имеют вид:
если
, то принимается гипотеза 
;
если
, то принимается гипотеза 
.
Повышение
порядка модели полезного сигнала может привести к уменьшению фазовой задержки,
вносимой фильтром Калмана и к уменьшению времени принятия решения о наличии или
отсутствии динамической составляющей в ошибке управления. Однако, это приведет
к усложнению реализации алгоритма принятия решения.
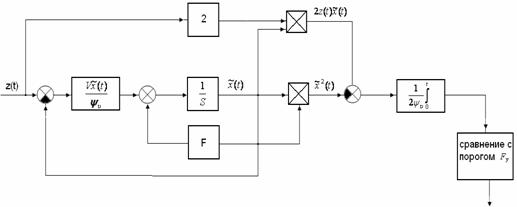
рис.
2 Структурная схема блока обнаружения
динамической ошибки
Для
регулирования полосы пропускания фильтра и изменения коэффициента передачи системы
вводится блок обнаружения динамической ошибки (см. рисунок 2) и блок принятия
решения. Блок принятия решения при обнаружении динамической составляющей в
ошибке управления расширяет полосу фильтра и увеличивает коэффициент передачи.
Это уменьшает влияние фильтра на точность работы системы. При малой величине
динамической ошибки полоса фильтра уменьшается и уменьшается коэффициент
передачи, что обеспечивает эффективное подавление помех.
Для
рассмотренной в работе [2] системы управления летательным аппаратом для
начального участка управления коэффициент передачи задается равным 130 1/с2,
а полоса пропускания фильтра Калмана = 0,5 Гц. Адаптация системы управления к величине
динамической составляющей ошибки управления включается при возрастании влияния
помех измерения. Учитывая, что система имеет второй порядок астатизма,
необходимо определить минимальное и максимальное значения коэффициента передачи, при которых
обеспечивается устойчивость системы управления. Были определены следующие
параметры фильтра и системы для номинального случая: полоса пропускания фильтра
Калмана = 2 Гц и коэффициент
передачи Кр = 4,5 1/с2 . Для эффективного подавления помех измерения
полоса пропускания фильтра Калмана = 1Гц и Кр = 2.5 1/с2. Для обеспечения отработки
управляющих воздействий с меньшей динамической ошибкой полоса пропускания
фильтра Калмана = 3Гц и Кр = 8 1/с2.
Осуществлено исследование полученной адаптивной системы с фильтром Калмана в
среде Matlab. Результаты приведены на рисунке 3.
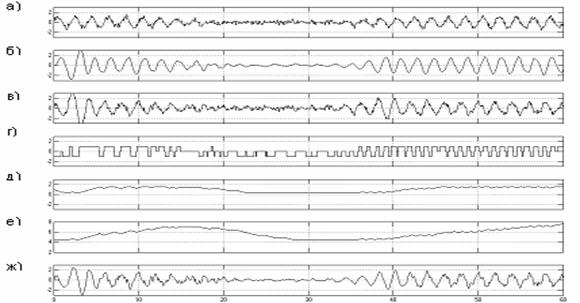
Рис.
3 Результаты моделирования а) входной сигнал: б) выходной сигнал в) сигнал
ошибки на входе фильтра г) сигнал с выхода блока
принятия решения д) S е) Кр ж) сигнал ошибки с выхода фильтра
Таким
образом, в работе рассмотрены вопросы адаптации системы управления с фильтром
Калмана к управляющим и возмущающим воздействиям в реальной помеховой
обстановке. При отсутствии динамической составляющей в ошибке управления в
системе обеспечивается уменьшение полосы пропускания фильтра Калмана и
уменьшение коэффициента передачи системы. При наличии динамической ошибки
осуществляется расширение полосы фильтра и увеличение коэффициента передачи.
Проведенное моделирование работы рассмотренной адаптивной системы управления с
фильтром Калмана показало эффективность предложенных технических решений.
Литература
1.
Э. Сейдж, Дж. Мелса Теория оценивания и её применение в связи и
управлении. – М.: Связь,1976.
2.
3.