Об управляемости многоэтапных динамических процессов с подвижными концами

В.Р. Барсегян,
 в.н.с., проф. каф. механ. ЕГУ, д.ф.-м.н., barseghyan@sci.am,

Т.В. Барсегян,
 н. с., к.ф.-м.н., t.barseghyan@mail.ru,  

Инст. механики НАН Армении, ЕГУ, г. Ереван, Армения

Рассматриваются вопросы управляемости многоэтапных (составных и поэтапно меняющихся) динамических процессов с подвижными концами. Получены необходимые и достаточные условия вполне управляемости составной (и поэтапно меняющейся) линейной стационарной системы, выраженные непосредственно через исходные параметры системы, которые сравнимы по завершенности с аналогичными условиями Калмана. Выявлено, что вследствие использования полезных свойств каждой из подсистем можно получить новое свойство вполне управляемости многоэтапного динамического процесса с подвижным концом, которым возможно не обладает ни одна из этих подсистем. Показано, что невырожденное линейное стационарное преобразование не влияет на свойство управляемости многоэтапных динамических процессов с подвижными концами.

 

The issues of controllability of multi-stage (compounded and stage by stage changing) dynamic processes with movable endpoints are considered. Necessary and sufficient conditions for complete controllability of multi-stage linear stationary systems are derived, which are comparable with analogues Kalman conditions. It's revealed that by the usage of helpful properties of each subsystem a new property of complete controllability of multi-stage dynamic processes with movable endpoints can be obtained, such a new property that any of these subsystems may not possess. It's shown that nonsingular linear stationary transformation doesn't affect the complete controllability property of multi-stage dynamic processes with movable endpoints.

Введение

Многие процессы управления из различных областей науки и техники предъявляют все новые требования к математическим моделям систем управления и наблюдения, ставят новые задачи более широкого класса динамических систем. В частности, одной из важнейших задач развития высокотехнологического производства является задача повышения уровня автоматизации в целях значительного сокращения применения ручного, малоквалифицированного и тяжелого труда путем использования автоматизированных технологических процессов управления непрерывного и поэтапного действия.

Для проектирования и исследования современных автоматизированных технологических процессов, разными авторами, в частности, предложены математические модели более сложных динамических систем управления фиксированной структуры с выделенной переменной структурой и возможностью в них мгновенного изменения значения параметров и мгновенной смены поведения. Поэтому возникает необходимость изучения фундаментальных проблем математической теории управления и наблюдения таких систем, появляется потребность в разработке новых или более эффективных методов исследования различных задач для таких систем, в частности, составных или поэтапно меняющихся динамических систем, в которых эффектом многоэтапности пренебречь нельзя. Интерес к задачам управления составных или поэтапно меняющихся динамических систем связан также с широкими возможностями современной вычислительной и измерительной техники, которые позволили изучать наиболее адекватные математические модели управляемых или наблюдаемых процессов.

Как в обычных задачах управления [1-3], так и в задачах управления многоэтапными динамическими процессами принципиальными являются вопросы управляемости таких систем. Некоторые вопросы управляемости и наблюдаемости систем переменной структуры и кусочно линейых импульсных систем исследованы, в частности, в работах [3-12]. И несмотря на возрастающий интерес к многоэтапным динамическим системам, достигнутых успехах в развитии теории, ощущается недостаток конструктивных методов и практических инструментов для исследования управляемости и разработки управления таких динамических систем. В частности, критерии управляемости для многоэтапных динамических систем с подвижными концами даже в линейном стационарном случае результатов, сравнимых по завершенности с критериями Калмана, нет.

В данной работе получены необходимые и достаточные условия вполне управляемости с подвижными концами составной (и поэтапно меняющейся) линейной стационарной системы с изменением размерности фазового вектора и вектора управления, которые выражены непосредственно через исходные параметры системы и сравнимы по завершенности с известными условиями Калмана. Выявлены также некоторые качественные свойства.

1. Постановка задачи

Рассмотрим управляемый процесс, динамика которого на интервале времени ,  описывается -мерными линейными стационарными дифференциальными уравнениями

                                                      (1)

с условием связи

,    ().                        (2)

Здесь , –фазовый вектор системы, ,  ()–матрицы параметров системы; –управляющие воздействия, соответственно, с размерностями  , , , - мерные, - мерные матрицы, а -мерный вектор столбец. Предполагается, что матрицы ,  и вектор  известны, а матрицы  ()  такие, что существуют , т.е. .

Предполагается, что заданы начальное  состояние и промежуточные моменты времени

.

Пусть с помощью измерительных устройств измеряются некоторые величины рассматриваемой составной системы, т.е. задан выход (результат измерения). Обозначим через - выходной вектор, компоненты которого являются линейными комбинациями фазовых координат , т.е.

,                                                                  (3)

где постоянная матрица  имеет размерность ().

Целью управления является приведение выходного вектора  к моменту  в заданное состояние

         .                                                          (4)

Условие (4) означает, что фазовая точка  должна быть приведена в момент времени  на  – мерное подпространство - мерного пространства.

Рассмотрим частный случай составной системы (1) с условиями связи (2), предполагая, что

1) размерности фазового вектора  и вектора управления  не меняются, то есть , , при ,

2) матрицы ,  и вектор-столбец  удовлетворяют условиям

 и ,

которые обеспечивают стыковки траектории системы в промежуточные моменты времени  (конец движения предыдущего этапа является началом следующего этапа).

Tогда вместо системы (1), (2) будем иметь следущую поэтапно меняющуюся линейную стационарную систему

,                                                         (5)

с промежуточными условиями в моменты времени  

         .

Результат измерения (выходной вектор) задается в виде         

,                                                                             (6)

где постоянная матрица  имеет размерность ().

Целью управления, для системы (5)-(6), является приведение вектора  к моменту  в заданное состояние

.                                                            (7)

Сформулируем определение вполне управляемости составной системы с подвижным концом (1)-(3) на отрезке времении  следующим образом.

Определение. Составная система (1) с промежуточными условиями связи (2) называется вполне управляемой по  на отрезке времени , если для любых начальных  и конечных  состояний можно найти набор управлений ,  такой, что решение , начиная из состояния  и удовлетворяя промежуточным условиям связи (2), в момент времени  удовлетворяет условию .

Вполне управляемая составная система (1), (2) с подвижным концом (4) обладает тем свойством, что с помощью соответствующего набора допустимых управлений ее можно перевести из любого заданного  начального  состояния в желаемое (заданное)  конечное состояние, удовлетворяя условиям связи (2).

Задача заключается в том, чтобы найти условия, при которых система (1)-(3), будет вполне управляемой с выходом (4) на отрезке времени .

2. Критерии управляемости многоэтапных динамических процессов

Получены необходимые и достаточные условия вполне управляемости с выходом (с подвижным концом) составной и поэтапно меняющейся линейной стационарной системы, выраженные непосредственно через исходные параметры системы. Эти условия выражены через ранги матриц управляемости, соответственно.

Справедливы следующие теоремы.

Теорема 1. Для того чтобы система (1)-(3) была вполне управляемой по  на промежутке времени , необходимо и достаточно, чтобы ранг матрицы

      (8)

был равен , где

;    ,                            (9)

       ,

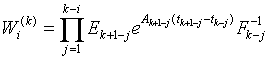
а числа  обусловлены кратностями собственных значений матрицы  .

Размерность матрицы  равна 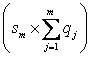, где .

Отметим, что (8) можно представить в виде

                                                                                   (10)

где     

.

Здесь постоянные матрицы   определяются по формле (9).

Формула (10) выражает связь между матрицей управляемости  (8) системы (1)-(3) по выходу  и матрицей управляемости  составной системы (1)-(2) [5, 9].

Теорема 2. Для того чтобы система (5)-(6) была вполне управляемой по  на промежутке времени  необходимо и достаточно, чтобы ранг матрицы

                                        (11)

был равен , где

                       ,                                         (12)

        ,

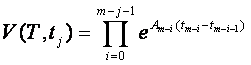
а числа  обусловлены кратностями собственных значений матрицы  .

Размерность матрицы  (11) равна 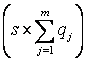. А матрица управляемости  системы (5)-(6) по выходу  представляется в виде

                                                                                          

где

и является матрицей управляемости системы (5) [5, 6, 9]. Здесь постоянные матрицы   определяются по формуле (12).

Отметим, что условия управляемости многоэтапных динамических процессов с подвижными концами сравнимы по завершенности с известными условиями Калмана [1, 2].

Известно [5, 6, 9], что составная система (или поэтапно меняющаяся система), образованная из не вполне управляемых (наблюдаемых) подсистем  на отдельных отрезках времени с соответствующими промежуточными условиями связей,  может быть вполне управляемой (наблюдаемой) на всем отрезке времени. Следовательно, согласно формуле (10) выявлено, что вследствие использования полезных свойств каждой из подсистем можно получить новое свойство вполне управляемости многоэтапного динамического процесса с подвижным концом, которым возможно не обладает ни одна из этих подсистем.

3. Влияние невырожденного преобразования на свойства управляемости

Учитывая, что преобразованная составная (и поэтапно меняющаяся) линейная система, полученная с помощью невырожденного линейного преобразования и исходная система эквивалентны, то есть одинаковым входным воздействиям соответствуют одинаковые выходные величины [7], рассмотрим влияние невырожденного линейного преобразования на свойства управляемости составной линейной стационарной системы с подвижным концом.

Для составной системы с подвижным концом (1)-(3) рассмотрим невырожденные линейные стационарные преобразования фазовых переменных:

,   ,                                     (13)

где - мерные матрицы и .

Выполняя преобразование (13), получим

                                      (14)

,                                           (15)

,                                                          (16)

где преобразованные матрицы системы вычисляются по формулам

,                ,   ,                  ,             .

Матрица управляемости преобразованной составной системы (1)-(3), согласно формуле (10), будет

.

Но так как  

,                 ,

то получим

,

то есть  матрицы управляемости исходной (1)-(3) и преобразованной (14)-(16) составной линейной стационарной системы с подвижными концами совпадают.

Таким образом, невырожденное преобразование не влияет на свойство управляемости составной линейной стационарной системы с подвижным концом.  Отметим, что при проектировании многоэтапных динамических процессов с подвижными концами с помощью невырожденного преобразования, сохраняющего свойство управляемости, удобно будет выбрать определенный базис в пространстве состояний с тем, чтобы матрицы параметров системы имели хорошую (удобную при вычислении и при моделировании системы) форму.

Заключение

Полученные необходимые и достаточные условия вполне управляемости многоэтапных динамических процессов с подвижными концами имеют важные теоретическое и прикладное значения. Эти условия выражены непосредственно через исходные параметры системы и могут иметь широкое практическое применение. Выявлено, что вследствие использования полезных свойств каждой из подсистем можно получить новое свойство вполне управляемости многоэтапного динамического процесса с подвижным концом, которым возможно не обладает ни одна из этих подсистем. Показано, что при проектировании многоэтапных динамических процессов с подвижными концами с помощью невырожденного преобразования, сохраняющего свойство управляемости, можно выбрать определенный базис в пространстве состояний с тем, чтобы в этом базисе матрицы параметров системы имели хорошую (удобную для вычисления и моделирования) форму.

Литература

1.  Калман Р. Об общей теории систем управления. Труды I Конгреса ИФАК, т. 2. Изд-во АН СССР, Москва, 1961, с. 521-547.

2.  Красовский Н.Н. Теория управления движением. М.: Наука, 1968, 476 с.

3.  Забелло Л.Е. Об управляемости линейных нестационарных систем, Автоматика и телемеханика, 1973, № 8, с. 13–19.

4.  Барсегян В.Р. Об условиях наблюдаемости поэтапно меняющихся управляемых линейных систем. Вестник Тамбовского университета. Серия: Естественные и технические науки. 2015. Т. 20. №5.  С. 1050-1055.

5.  Барсегян В.Р., Барсегян Т.В. Критерий управляемости линейных стационарных систем переменной структуры. Проблемы динамики взаимодействия деформируемых сред. Труды VIII международной конференции. Сентябрь 22-26, 2014, Горис-Степанакерт, с. 83-87.

6.  Барсегян Т.В. Об условии вполне управляемости поэтапно меняющейся линейной стационарной системы. Известия НАН РА. Механика, 2015, № 1, с.81-90.

7.  Барсегян Т.В. О замене базиса в пространстве состояний и влиянии на свойства управляемости составной линейной стационарной системы. Проблемы динамики взаимодействия деформируемых сред. Труды VIII международной конференции. Сентябрь 22-26, 2014, Горис-Степанакерт, с. 88-92.

8.  Barseghyan V.R. Control of stage by stage changing linear dynamic systems. Yugoslav Journal of Operations Resarch. 2012, Vol. 22, № 1, pp. 31-39. 

9.  Barseghyan V.R. "On the controllability and observability of linear dynamic systems with variable structure, "2016 International Conference Stability and Oscillations of Nonlinear Control Systems (Pyatnitskiy's Conference), Moscow, Russia, 2016, pp. 1-3.   http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=7541163&isnumber=7541147

10.  Johansson M. Piecewise Linear Control Systems. Spriger, 2003, X, 220 p.

11.  Hong Shi and Guangming Xie. Controllability and Observability Criteria for Linear Piecewise Constant Impulsive Systems. Journal of Applied Mathematics. Volume 2012 (2012), Article ID 182040, 24 pages. http://dx.doi.org/10.1155/2012/182040

12.  Dengguo Xu. Controllability and Observability of a Class of Piecewise Linear Impulsive Control Systems. Advances in Computer, Communication, Control and Automation. LNEE Vol. 121, 2012, pp. 321-328.