Квантовые D-алгоритмы и центральная проблема современной дискретной математики[1]

П.А. Правильщиков,
в.н.с., к.т.н., с.н.с., pavelp@ipu.ru,
ИПУ РАН, г. Москва

В первом докладе автора«Центральная проблема современной дискретной математики и квантовый генератор тестов» приведено описание новой модели вычислений в виде идеального квантового генератора тестов (КГТ). Данный доклад можно рассматривать как продолжение первого. В нём приводится описание квантовых D-алгоритмов, «заточенных» под новую модель вычислений. Описание квантовых D-алгоритмов приведено на примерах решения логических уравнений, что позволяет решить в общем виде известную SAT-проблему. Показано, что решение SAT-проблемы с помощью квантовых D-алгоритмов на базе КГТ позволяет утверждать, что решение SAT-проблемы требует полиномиальных по объёму вычислительных ресурсов.

In the first report of the author «The central problem of modern discrete mathematics and the quantum generator of tests» the description of new computing model in the form of the ideal quantum generator of tests (QGT) is resulted. The given report can be considered as continuation of the first. In this report the description of the quantum D-algorithms fitted under new computing model is resulted. The description of quantum D-algorithms is resulted on examples of the decision of the logic equations that allows to solve a known SAT-problem in a general view. It is shown that the decision of a SAT-problem by means of quantum D-algorithms on the basis of QGT allows to assert, that the decision of a SAT-problem demands polynomial computing resources.

1. Постановка задачи

Пусть задано логическое уравнение, например, уравнение вида:
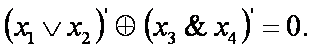(1)
Уравнение (1) можно переписать следующим образом:
(2)

Тогда левая часть (2) может быть реализована в виде логической сети комбинационного устройства (КУ), показанного на рис. 1.

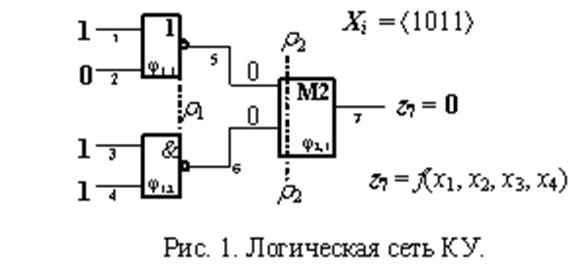
Логические элементы КУ разбиты на множества M₁ = {j_1,1, j_1,2} и M₂ = {j_2,3}, относящихся к двум рангам сети : r = 1 и r = 2. Символ R обозначает число рангов. Для КУ (рис. 1) R = 2. Так же могут быть разбиты на ранги и логические операторы уравнения (2). Обратная задача (по сути SAT-проблема) в случае решения логического уравнения (т.е. SAT-проблемы) формулируется следующим образом. Пусть задано уравнение, например, уравнение (2), или задано эквивалентное КУ, у которого задано значение на выходе z_j. Например, для КУ на рис. 1 z₇ = 0. Требуется найти кортеж X_i = áx₁, …, x_nñ, на котором заданное уравнение выполняется. Для уравнения (2) число аргументов n = 4. Примером такого кортежа служит вектор X_i = á1011ñ для уравнения (1) и (2), а также для КУ на рис.1. Так, если найден вектор X_i = á1011ñ, то уравнение (2) будет выполняться:

Для решения задачи будут использованы QD-алгоритмы, выполняющие полный перебора и основанные на новом неклассическом матричном исчислении кубических комплексов, которое является развитием класси-ческого исчисления кубических комплексов (D-исчисления). Напомним, что D-исчисление было разработано в 1966 г. американским математиком Дж. П. Ротом [1]. При решении примеров здесь для конкретности предполагается, что dim H = = 360.

2. Решение SAT-проблемы с помощью QD-алгоритмов

До начала процесса решения задачи предварительно следует выполнить подготовительные операции. Одной из них является ранжирование операций в логическом уравнении, например, в уравнении (2) ¾ см. [1].

Равносильное ранжирование может быть выполнено для эквивалентного КУ (см. рис. 1 в [1]). Затем выполняется запись конкатенаций для каждого ранга r. Здесь r = . Так как решение задачи (т.е SAT-проблемы) будет проиллюстрировано на примере эквивалентного КУ (см рис.1) и операция ранжирования уже выполнена для этого КУ, то для каждого ранга КУ на рис. 1 целесообразно выполнить запись конкатенаций строк сокращённых таблиц истинности [1,2]. Для первого ранга (r = 1) конкатенация
K₁ = K_ИЛИ-НЕ ║K_И-НЕ, где K_ИЛИ-НЕ — конкатенация строк сокращённой таблицы истинности для j_1,1 (ИЛИ-НЕ) (табл. 1 и рис. 1). Аналогичная конкатенация K_И-НЕ является конкатенацией строк такой же таблицы для j_1,2 (И-НЕ) ¾ см. табл. 2 и рис. 1.

K_ИЛИ-НЕ = s_1,1,1║s_1,1,2║s_1,1,3 = ║║.
K_И-НЕ = s_1,2,1 ║ s_1,2,2 ║ s_1,2,3 = ║║.

Тогда для ранга r = 1 конкатенация K_r = K₁ = K_ИЛИ-НЕ ║ K_И-НЕ имеет вид:

^{Kr = K1 =║║║║║. (3)}

Аналогично составляется и конкатенация K₂ для второго (последнего) ранга КУ Конкатенация K_r = K₂ — это конкатенация строк табл. 6 для элемента j_2,1 (M2), который отнесён ко второму рангу (r = 2) ¾ см. рис. 1 и табл. 6 в [1].

^{Kr = K2 =║ (4)}

В результате ещё до начала выполнения QD-алгоритма построены две конкатенации K₁ и K₂ . Их можно рассматривать как неотъемлемые характеристики логического уравнения (1) или (2).
Так как мы используем новое матричное D-исчисления, то поэтому табл. 1, 2 и 5 перепишем так, что их строки станут вектор-столбцами. Например, первую строку в табл. 2 запишем в виде вектор-столбца v₁, вторую — в ви-де вектора-столбца v₂ и, наконец, третью — в виде вектора-столбца v₃ :

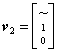, и .

Аналогично можно переписать и строки остальных таблиц (например, табл. 4). Однако подобная запись вектор-столбцов достаточно громоздка и в тексте доклада может занимать много места. Поэтому в целях экономии объёма доклада вместо каждого вектор-столбца можно использовать транспонированную вектор-строку. Например, те же векторы v₁, v₂ и v₃ ¾ см. выше (3) можно записать в следующем виде:

v₁ = [0 0 1]^T; v₂ = [~ 1 0]^T; v₃ = [1 ~ 0]^T. (5)

Аналогично можно записать и конкатенации K₁ и K₂ в форме транспонированных вектор-строк:

(6) (7)

В (6) и (7) символы «║» опущены, так как в них нет необходимости при выполнении пересечения C_q Ç K_r, где C_q ¾ куб, записанный в одном куните (например, в k_1,1). С кубом C_q осуществляется пересечение на шаге (q + 1). Запись конкатенаций в виде (5) и (6) позволяет на каждом шаге q QD-алго-ритма компактно осуществлять запись пересечения C_q Ç K_r. Подобная запись близка к классической записи при описании параллельно-последова-тельных D-алгоритмов [11], хотя куниты на рис. 2 представлены в виде столбцов, т.е. содержанием каждого кунита является вектор-столбец. Каждый блок QB_m реализует блочно-диагональную матрицу U^†_RБ-Д, . С математической точки зрения процесс пересечения представляет собой умножение блочно-диагональной матрицы U^†_RБ-Д,на соответствующий вектор-столбец (или на соответствующую транспонированную вектор-строку).
До начала выполнения QD-алгоритма необходимо также установить куниты квантового регистра в начальное состояние, например, в состояние 0 (все спины ). Для этого могут быть использованы простые схемы, описание которых приводится в [3-5]. Возможны и другие варианты схем. Вектор начального состояния кунита – вектор ¾ имеет вид:

(8)

После этого, можно начать пошаговое выполнение QD-алгоритма.

Шаг 1 (q = 1). Используя логический вентиль, реализующий соответствующую однородную или неоднородную блочно-диагональную матрицу в некоторый кунит k_m (например, k₁) записывается начальные куб С₀. Конкатенация K₂ в форме (6) записывается в другой кунит (например, k₂). После этого с помощью квантовой схемы (квантового вентиля), реализующуей матрицу U_RБ-Д,, выполняется пересечение C₀ Ç K₂. В записи классического параллельно-последовательного D-алгоритм третьего типа [11] пересечение C₀ Ç K₂ имеет вид:

(9)

При этом в первых 4-х координатах операции a_g не выполняются. В этом случае требуются всего шесть блоков пересечения – шесть классических блоков B_j. Выполнение процедуры фильтрации[2] и пролифирации – см. [7], по сути, выдаёт два куба C_1,1 и C_1,2 :

(10)

Запись C₀ Ç K₂ в случае QD-алгоритма, когда используются блочно-диагональные матрицы U_RБ-Д,, выглядит значительно сложнее. Это лишний раз свидетельствует о том, что квантовые явления практически невозможно мо-делировать на классическом компьютере и особенно в случае многих квантовых частиц. Так же практически невозможно моделировать поведение КК с помощью классического компьютера. Но если использовать матричное D-исчисление внешне всё выглядит компактно и благопристойно. Так, пересечение C₀ Ç K₂ (8) может быть записано:

(11)

Но если для пересечения C₀ Ç K₂ в случае (9) используется табл. 1 из нашего первого доклада, которая в том или ином виде хранится у нас в уме или в памяти классического компьютера, то в случае (11) используются гро-моздкие матрицы U^†_R,Б-Д, , которые образуются из подматриц, в качестве которых выступают элементарные матрицы Рота. Таким образом, в каждой матрице U^†_RБ-Д, блоком является унитарная матрица U^†_R ¾ матрица Рота (см. (4) в первом докладе автора). Здесь при выполнении QD-алгоритма приходится математически имитировать унитарную эволюцию, переводя исходное квантовое состояние двух кунитов в результирующее состояние :

= U^†_R,Б-Д,(). (12)

Сравнивая (9) и (11) заметим, что на первом шаге классического параллельно-последовательного D-алгоритма III типа при выполнении C₀ Ç K₂ (9) операции a_g в первых 4-х координатах не выполнялись. Это сделано для уменьшения числа блоков B_j и объёма ОП, т.е. экономит аппаратуру классического ускорителя. Здесь при описании QD-алгоритма память и блоки QB_m экономить не будем, так как «в гильбертовом пространстве много места» и один блок QB_m выполняет много операций a_g . Преимущество та-кого подхода состоит в том, что позволяет существенно экономить время ¾ см. [8]. В [8] показано, что при таком подходе параллельно-последователь-ный D-алгоритм IV типа может быть выполнен всего за один шаг, т.е. с временной сложностью в 1 вдеп и небольшими «накладными расходами». Теперь возвращаясь к (12) запишем состояние 2-х кунитов с учётом таб-лицы кодирования (см. табл. 2 в нашем первом докладе на данной конференции) в следующем виде:

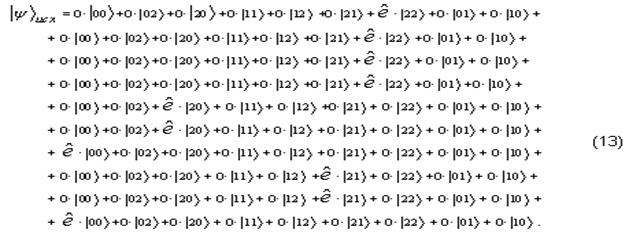
Подчеркнём, что подобная математическая имитация достаточно громоздка и связана со сложившимся математическим аппаратом квантовой механики[3]. В выражении (12) для символ «» обозначает единичный элемент, т.е. такой элемент, который замещает единицу в элементарной матрице Рота ¾ матрице U^†_R. Это объясняется тем, что при использовании блочно-диагональной матрицы U^†_RБ-Д, требуется соблюдать правило нормировки ¾ см. постулат 5 в [1]. Для выражения (12) численное значение символа , если опустить нулевые амплитуды, определяется уравнением: + +++ +++ ++ = 1, или 10×= 1. Отсюда = 0,1 и = » 0,316.

Таким образом, для выполнения первого шага (q = 1) нам понадобилось два кунита, в которых записаны вектор-столбцы, содержащие куб C₀ (кунит k₁) и конкатенацию K₂ (кунит k₂). Так же нам понадобился одна квантовая схема (квантовый вентиль), реализующий блочно-диагональную матрицу U^†_RБ-Д,= U^†_RБ-Д,10. Здесь = 10. Блочно-диагональная матрица U^†_RБ-Д,10 построена из 10 элементарных матриц Рота, которые выступают блоками (подматрицами) матрицы U^†_RБ-Д,10. Теперь необходимо получить результат умножения матрицы U^†_RБ-Д,10 на соответствующий вектор V_исх:
V_исх = [00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000]^T.

Произведение V_рез = U^†_RБ-Д,10 ´ V_исх имеет вид:

U_RБ-Д,10 ´ V_исх =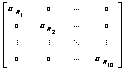´ . (14)

Учитывая свойства блочно-диагональных матриц U^†_R,Б-Д,, блоками которых матрицы U^†_R, можно осуществить умножение, аналогичное умножению (14) одной матрицы U^†_R на 10 разных векторов:
V_исх,1 = [00000000]^T; V_исх,2 = [00000000]^T ; V_исх,3 = [00000000]^T;
V_исх,4 = [00000000]^T; V_исх,5 = [00000000]^T; V_исх,6 = [00000000]^T;
V_исх,7 = [00000000]^T ; V_исх,8 =[00000000]^T ;V_исх,9 = [00000000]^T ;
V_исх,10 = [00000000]^T.

Эти 10 векторов образуют большой вектор V_исх ¾ см. выше. Другими словами, следует последовательно ( например, на классическом компьютере) получить следующие десять произведений: 1) V_рез,1 = U^†_R´V_исх,1;
2) V_рез,2 = U^†_R´V_исх,2; 3) V_рез,3 =U^†_R´V_исх,3; 4)V_рез,3= U^†_R ´V_исх,4; 5) V_рез,5 = =U^†_R´V_исх,5; 6) V_рез,6 = U^†_R´V_исх,6; 7) V_рез,7 = U^†_R´V_исх,7; 8) V_рез,8 = U^†_R´V_исх,8;
9) V_рез,9 = U^†_R´V_исх,9; 10) V_рез,10 = U^†_R´V_исх,10 .
Получив последовательно векторы V_рез,1 ¸ V_рез,10 , составим из них большой вектор-столбец V_рез, который является результатом произведения
U^†_RБ-Д,10 ´ V_исх = V_рез . Вектор V_рез имеет вид:
V_рез = [00000000 00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000]^T.
Тогда результирующий вектор имеет вид:

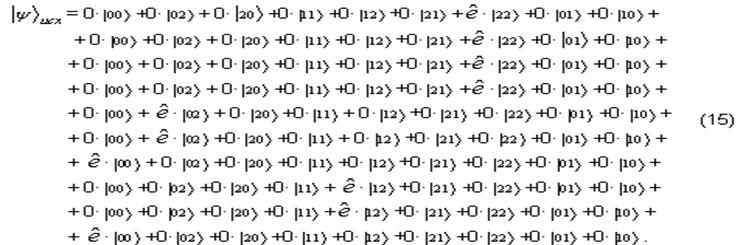
Так как в результирующем векторе получено 10 единичных элементов , то = » 0,316.
Теперь поясним физический смысл нашего математического умножения U^†_RБ-Д,10 ´ V_исх = V_рез ¾ см. (14). Будем предполагать, что для реализации кунитов k₁ и k₂ квантовых разрядов QR₁ и QR₂ (k₁ Î QR₁, а k₂ Î QR₂) ¾ см. рис. 2 ¾ используются спины тех или иных квантовых частиц. Поясним фи-зическую интерпретацию взаимодействия кунитов k₁ и k₂ с квантовым элементом Рота ¾ взаимодействия, которое реализует произведение (14). Физический смысл состоит в том, что квантовый элемент Рота, реализующий произведение U^†_RБ-Д,10 ´V_исх, выполняет поворот спина на определённый угол. Величина этого угла определяется величинами двух углов спинов, соответствующим состояниям кунитов k₁ и k₂. Конечно, в отличие от классической физики состояния кунитов может быть определено только с некоторой вероятностью.
Важной особенностью, сущностной чертой квантовой революции является использование аналоговых свойств КК. Именно об этом, рассуждая о КК и будущем науки, так убедительно пишет С. Ллойд [9, стр. 175]: «Наша классическая интуиция подсказывает, что аналоговые вычисления по сути своей непрерывны, а цифровые вычисления должны быть дискретными. Но когда дело касается квантовых вычислений, как, впрочем, и во многих других случаях, классическая интуиция нас подводит. Аналоговый квантовый компьютер и цифровой квантовый компьютер — это одно и то же устройство». По сути, в такой постановке задача становится аналоговой задачей. Но с учётом требований квантовой механики здесь она решается с помощью унитарных матриц. Если, например, исходное состояние двух спинов было «спин » ¾ см. (8), то в результате взаимодействия двух кунитов с квантовым элементом Рота спин, лежащий в основе кунита k₁ , будет повёрнут по часовой стрелке на соответствующий результирующему вектору V_рез угол. Таким, углом может быть, например, угол равный 45° или на угол равный 64,5°, либо на другой угол. Если, например, исходное состояние двух спинов было другим, не равным состоянию «спин » , то всё равно в результате взаимодействия спин кунита k₁ , будет повёрнут на соответствующий результирующему вектору V_рез угол либо по часовой стрелке, либо против часовой стрелки. Поворот может быть выполнен фотоном в энергией E = hn_k ¾ фотоном, взаимодействующим с квантовой частицей (например, с электроном, либо ионом атома). Изменяя частоту n_k фотона, а значит, и его энергию E, можно управлять спином частицы, поворачивая спин на нужный угол (следует, однако, подчеркнуть, что поворот будет выполнен с некоторой вероятностью).

В случае умножения на классическом компьютере нам потребовалось бы последовательно выполнить десять умножений типа (14)[4]. В случае КК или КвУ используется квантовый параллелизм, практически не увеличивающий объём аппаратуры.

Это во многом зависит ещё и от числа : чем больше , тем большей степени параллелизма можно достичь при выполнении многих элементарных операций a_g . Операции a_g в этом случае выполняются путём многократного умножения U^†_R ´ V_исх ¾ см. выше. В [10] утверждается, что в случае перехода от кубитов (= 2) к кутритам = 3) при решении одной и той же задачи объём квантовой аппаратуры уменьшился более чем в 5 раз. В нашем случае – в случае первого шага QD-алгоритма необходимы куниты k_1,1 и k_2,1, которые, по крайней мере, имеют размерность не менее dim H = == 10. На этом шаге параллельно выполняется 10 операций a_g и используется только один блок QB₁ (= 1, где ¾ число блоков QB_m). Блок QB_m имеет два входа, которые связаны с кунитами k_1,1 и k_2,1 . В случае использования классического специализированного процессора-ускорителя на шаге 1 понадобилось бы, по крайней мере, 6 блоков пересечения (блоков B_j)¾ см. пересечение (9) и пояснения к этому пересечению. Здесь время выполнения первого шага Dt₁ = 1 вдеп, так как все 10 операций выполняются параллельно.

После выполнения пересечений на первом шаге, необходимо выполнить процедуру фильтрации и пролифирации. Для выполнения этой процедуры используются однородные и неоднородные блочно-диагональные матрицы, подматрицами которых являются матрицы элементов CNOT, единичная матрица I, матрица Тоффоли и матрица Фредкина[5] ¾ см. [1]. В результате этой процедуры будут получены те же кубы C_1,1 и C_1,2 ¾ см. (10), записанные в куните k₁. Временные «накладные расходы» относительно не велики и составляют k×Dt₁, где k ¾ константа, зависящая от выбранной квантовой схемы фильтрации и пролифирации, а также схем удаления «квантового мусора» [3, стр. 208]. Существует вариант такой схемы, где k = 3, но возможны и более быстрые схемы. Примерно такие же «накладные (полиномиальные) расходы» связаны и с квантовой аппаратурой.

Шаг 2 (q = 2). На втором шаге выполняется пересечение каждого из двух кубов C_1,1 и C_1,2 (9), полученных на первом шаге, с конкатенацией K₁ (1). В случае классического параллельно-последовательного D-алгоритм третьего типа [11] пересечение C_1,1 Ç K₁ и пересечение C_1,2 Ç K₁ имеет вид:

(16)

После выполнения классической операции фильтрации и пролиферации получим следующие кубы:

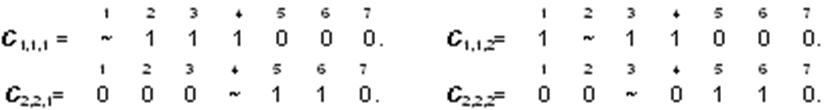(17)

Кубы C_1,1,1, C_1,1,2 , C_2,2,1 и C_2,2,2 в координатах 1, 2, 3 и 4 содержат четыре не полностью определённых входных набора , , и :

	1	2	3	4
=	á~	1	1	1ñ;

	1	2	3	4
=	á1	~	1	1ñ;

	1	2	3	4
=	á0	0	0	~ñ;

	1	2	3	4	(18)
=	á0	0	~	0ñ.

Из наборов , , и получают = {X₁, X₂, X₃, X₈, X₁₂, X₁₆ }, где X₁ = á0000ñ, X₂ = á0001ñ, X₂ = á0010ñ, X₈ = á0111ñ, X₁₂ = á1011ñ, X₁₆ = á1111ñ; Каждый X_i Îрешает SAT-проблему для уравнения (1) и (2) .
На втором шаге QD-алгоритма в соответствии с постулатом 1 достаточно построить только один набор X_i Î. Пересечения C_1,1 Ç K₁ и C_1,2 Ç K₁ по внешнему виду мало отличается от (16). И хотя по внешней форме различия между (16) и (19) не велики, содержательно пересечения (16) и (19) сильно различаются. Все 38 операций a_g ¾ элементарных операций пересечения ¾ выполняются по-разному. В (16) каждая операция a_g выполняется отдельным блоком B_j, построенным из классических элементов и, так как с ростом размерности логических уравнения вида (1) или (2), либо размерности соответствующего КУ (см. рис. 1), то число блоков B_j возрастает экспоненциально (аппаратур ускорителя возрастает экспоненциально). В случае выполнения (19) на втором шаге QD-алгоритма пересечение траспонированного вектора, содержащего два куба: C_1,1 и C_1,2 с траспонированным вектором, содержащем две конкатенации K₁ выполняется с помощью матриц U^†_RБ-Д,.

^1

^2

^5

^1

^2

^5

^1

^2

^5

^3

^4

^6

^3

^4

^6

^3

^4

^6

^7

C1,1=

[~

~

^0

~

~

^0

~

~

^0

~

~

^0

~

~

^0

~

~

^0

^0]T

^K^1 =

^[^0

^0

^1

^~

^1

^0

^1

^~

^0

^0

^~

^1

^~

^0

^1

^1

^1

^0

^~]T

^Ç

^–

^–

^–

^–

^–

^–

^–

^–

^–

^–

^–

^–

^–

^–

^–

^–

^–

^–

^–

C2,1=

^[^0

^0

^Æ

^~

^1

^0

^1

^~

^0

^1

^~

^Æ

^~

^0

^Æ

^1

^1

^0

^0]T

(19)

^1

^2

^5

^1

^2

^5

^1

^2

^5

^3

^4

^6

^3

^4

^6

^3

^4

^6

(19) ^7

C1,2 =

[~

~

^1

~

~

^1

~

~

^1

~

~

^1

~

~

^1

~

~

^1

^0]T

^K^1 =

^[^0

^0

^1

^~

^1

^0

^1

^~

^0

^0

^~

^1

^~

^0

^1

^1

^1

^0

^~]T

^Ç

^–

^–

^–

^–

^–

^–

^–

^–

^–

^–

^–

^–

^–

^–

^–

^–

^–

^–

^–

C2,2 =

^[^0

^0

^1

^~

^1

^Æ

^1

^~

^Æ

^0

^~

^1

^~

^0

^1

^1

^1

^Æ

^0]T

Для выполнения (19) необходимо выполнить 38 операций a_g. (заметим, что в этом случае размерность dim H = = 9´38 =342, что меньше заданной в постановке задачи величины = 360.). Каждая операция a_g выполняется унитарной матрицей Рота ¾ матрицей U_RБ-Д,. Все 38 операций a_g выполняются одним блоком QB_m. Физически это означает поворот спина квантовой частицы, которая соответствует куниту k_1,1, куда и переписывается результат, на определённый угол.
После выполнения операции фильтрации и пролиферации будут получены такие же кубы, как и кубы C_1,1,1 , C_1,1,2 , C_2,2,1 и C_2,2,2 ¾ см. (18). Их можно записать в виде вектор-столбцов:

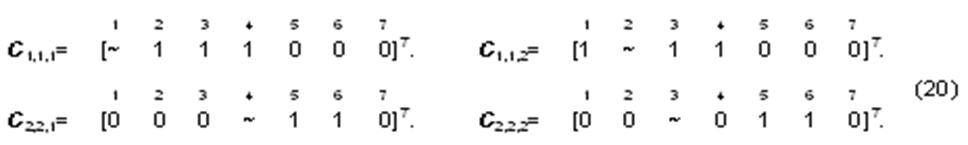
Все кубы в (19) расположены в одном куните k_1,m.

Подготовка к процессу измерения. Сравнивая (17) и (20) следует отметить существенные различия, связанные с тем, что значения в координатах кубов (20) могут быть получены в процессе измерения только с вероятностью. При этом в процессе измерения для всякого кунита k_1,m или k_2,m можно получить только одно значение. В связи с этим в случае QD-алгоритма можно получить только один не полностью определённый входной набор из наборов ,, и ¾ см. выше. Выберем набор , содержащийся в первых четырёх координатах куба C_1,1,1 . Набор в соответствии с постулатом 1 в [1] будет решением SAT-проблемы для уравнения (1) и (2). Тогда, удаляя квантовый мусор, следует переписать куб C_1,1,1 в n свободных кунитов . Здесь n – число независимых переменных в уравнении (здесь n = 4). Перепишем куб C_1,1,1 четыре раза, например, в куниты k_1,3 , k_1,4 , k_1,5 и k_1,6 . Это можно сделать, используя блочно-диагональные матрицы, у которых в качестве подматриц используются матрицы Тоффоли. Здесь матрицы Тоф-фоли используются для выполнения функции «повторение» (прямое копирование состояния квантовых разрядов в КК запрещено [3, стр. 46-47]). Следующий шаг подготовки состоит в том, чтобы единичные элементы «» максимально увеличить, т.е. превратить в единицу. Для этого следует использовать неоднородную блочно-диагональную матрицу, у которой в качестве подматрицы используется одна единичная матрица U^†_I (9´9) [3, стр. 96]. Остальные подматницы ¾ это матрицы U^†_обмена. Каждая матрица позволяет вместе с кунитом k_1,m , в котором записаны нули, довести символ «» в куните, например, k_1,3 до единицы. Это позволит в результате измерения получить нужное значение переменной x₁ (в данном случае это «~») . Те же действия выполняются и для кунитов k_1,4 , k_1,5 и k_1,6 . Это позволяет получить в результате измерения значения переменных x₂, x₃, x₄ . В результате будет получен один набор X₁ = á ~ 1 1 1 ñ . Таким образом, будет найдено решение SAT-проблемы для логического уравнения вида (1) или (2). Для этого потребовалось вдеп, где ¾ константа, учитывающая накладные расходы. Это означает, что временная сложность решения SAT-проблемы полиномиальна. Полиномиальна и аппаратная сложность: число кунитов не более 2(n + ᴂ), где n ¾ число переменных в уравнении, а ᴂ ¾ константа, учитывающая накладные расходы на выполнение схем, реализующих операции фильтрации и пролифирации, а также схем, выполняющих операции по подготовке к процедуре измерения. Таким образом, число кунитов и число квантовых вентилей, реализующих блочно-диагональные матрицы, является полиномиальным. Это и является главным результатом доклада.

Литература

1. Roth J.P. Diagnosis of automata failures: a calculus and method // IBM Journal of Research and Development. 1966. № 7 (July). P. 18-32.

2. Карибский В.В., Пархоменко П.П., Согомонян Е.С., Халчев В.Ф. Основы технической диагностики. Кн. 1. М.:"Энергия", 1976. — 346 с.

3. Нильсен М., Чанг И. Квантовые вычисления и квантовая информация: Пер. с англ.— М.: Мир, 2006. — 824с.

4. Прескилл Дж. Квантовая информация и квантовые вычисления (Том I). Москва-Ижевск: ИКИ (НИЦ Регулярная и хаотическая динамика), 2008. — 464 стр.

5. Кайе Ф., Лафламм Р., Моска М. Введение в квантовые вычисления. — М.-Ижевск: НИЦ «Регулярная и хаотическая динамика», Институт компьютерных исследований, 2009. — 360 с.

6. Кайе Ф., Лафламм Р., Моска М. Введение в квантовые вычисления. — М.-Ижевск: НИЦ «Регулярная и хаотическая динамика», Институт компьютерных исследований, 2009. — 360 с.

7. Правильщиков П.А. Закон сохранения перебора и естественный параллелизм D-алгоритмов для построения тестов и моделирования в технической диагностике. // Автоматика и телемеханика. 2004. № 7. Стр. 156-199.

8. Правильщиков П.А. "Параллельные D-алгоритмы и закон сохранения перебора для них". // Оборонный комплекс ― научно-техническому прогрессу России". М.: НТЦ "Информтехника". 2000, .№ 4 (стр. 103-116).

9. ^{Ллойд С. Программируя Вселенную: квантовый компьютер и будущее науки / Пер. с англ. — М.: Альпина нон-фикшн, 2013. — 256 с. (См. стр. 175)}

10. B. P. Lanyon, M. Barbieri and all. Simplifying quantum logic using higher-dimensional Hilbert spaces. // Nature Physics, Vol. 5, No. 2. (2008), pp.134-140.

---

[1] Данный доклад является продолжением доклада автора «Центральная проблема современной дискретной математики и квантовый генератор тестов» на этой же конференции CAD/CAM/PDM - 2014. В нём используются те же понятия и обозначения, что и в первом докладе.

[2] Процедура фильтрации позволяет оставить непустые кубы и удалить пустые [1].

[3] Так, в классической механике для математической имитации движения мы используем привычный аппарат элементарной алгебры и арифметики. Например, пусть требуется определить время прибытия из пункта A в пункт B, если расстояние между ними 200 км и средняя скорость v движения автомобиля 80 км/час. Для определения времени придётся разделить S на v, т.е. 200 : 80 = 2,5. Иными словами, потребуется 2 часа 30 мин., чтобы прибыть из A в B, если не произойдёт чего-то непредвиденного (например, ремонт дороги или ДТП). В квантовой механике и в теории квантовых вычислений в соответствии с (12) мы определяем унитарную эволюцию, т.е. переход из одного состояния _исх в другое состояние _рез , но для этого используем громоздкий аппарат линейной алгебры и матричного исчисления.

[4] Можно, конечно, выполнять произведения параллельно с использованием проблемно-ориентированного классического процессора-ускорителя [11-14]. Но объём аппаратуры ускорителя в этом случае будет экспоненциально возрастать по мере увеличения размерности индивидуальной задачи выполнимости для логических уравнений (т.е. SAT-проблемы).

[5] Известно, что элемент Фредкина является универсальным логическим элементом. Как показано в [3, стр. 207-208] с помощью этого элемента можно реализовать функции AND, NOT, CROS-SOVER и FANOUT, так что с помощью комбинации элементов Фредкина можно моделировать любую классическую схему. К этому автор может добавить, что с помощью комбинации блочно-диагональных матриц U^†_Б-Д,Fr, так же можно моделировать любую классическую схему. Подматрицами матриц U^†_Б-Д,Fr, являются матрицы U^†_Б-Д,Fr, описывающие функционирование элемента Фредкина. При этом матрицы U^†_Б-Д,Fr,могут быть не однородными. Элемент Фредкина часто используется также для удаления квантового мусора.