Центральная проблема современной дискретной математики и квантовый генератор тестов

П.А. Правильщиков,
в. н. с., к.т.н., с.н.с., pavelp@ipu.ru
ИПУ РАН, Москва

Кратко рассмотрены возможные социальные и технологические последствия квантовой революции в области вычислительной техники, САПР и технической диагностики. Особенное внимание обращено на трунорешаемые (NP-полные) задачи в области CAD, CAM, PDM, цифрового САПР и технической диагностики, так как появление квантовых компьютеров (КК), квантовых ускорителей (КвУ) и квантовых алгоритмов может предоставить практически неограниченные вычислительные ресурсы для их решения. Решение хотя бы одной из класса NP-полных задач с полиномиальными ресурсами, например, проблемы выполнимости логических уравнений (SAT-проблемы) означает решение центральной проблемы (ЦП) современной дискретной математики. Во второй части доклада приводится описание квантовых D-алгоритмов для решение SAT-проблемы с использованием полиномиальных вычислительных ресурсов.

Possible social and technological consequences of quantum revolution in the area of computers, CAD and engineering diagnostics are is short considered. The especial attention is turned on intractable (NP-complete) problems in the field of CAD, CAM, PDM, САПР and engineering diagnostics as occurrence of quantum computers, quantum accelerators and quantum algorithms can give almost unlimited computing resources for their decision. The decision at le-ast one of a class of NP-complete (NP-hard) problems with polynomial resources, for example, SAT-problem, means the decision of the central problem of modern discrete mathematics. The description of quantum D-algorithms for the decision of a SAT-problem with use polynomial computing resources is resulted.

Введение

Сегодня в области вычислительной техники (ВТ) происходит очередная революция и это революция квантовая. Квантовая революция касается не только отказа от классической физики, лежащей у основе традиционных классических компьютеров, и перехода к квантовой механике, лежащей в основе квантовых компьютеров (КК). Эта революция также связана не только с количественным увеличением важнейших параметров компьютеров, таких как производительность, объём памяти. Квантовая революция в отличие от многих предшествующих революций в ВТ затрагивает также глубокие теоретические основы computer science. Но и это ещё не всё. С появлением первых коммерчески доступных КК и КвУ мы оказываемся на грани великих перемен. Ранее считалось, что для них нужны "тысячи веков". Однако некоторые математики и футурологи пришли к другому выводу: квантовая революция в ВТ действительно несёт великие перемены в нашей жизни. Они произойдут в ближайшие 20-25 лет [1].
Некоторые из тех, кто осознал неизбежность этих перемен, считают, что им было бы комфортнее, если бы от этих сверхъестественных событий нас отделяла тысяча лет. Многие заслуженные ученые выражают озабоченность потенциально катастрофическими технологиями, которые попадают в руки людей. В числе этих технологий находится и вопрос создания искусственного суперинтеллекта. Необходимо подчеркнуть, что каждый революционный прорыв в мире технологий (в том числе и квантовая революция) ¾ прорыв, с которым мы с энтузиазмом сталкиваемся впервые, может оказаться губительным для человека[1]. Сугубая причина перемен заключается в том, что квантовая революция неизбежно ведёт к созданию сущностей с интеллектом, превышающим человеческий. Доводом в пользу того, что этот интеллектуальный прорыв обязательно произойдёт, служит и то, что наука может достичь такого прорыва разными путями, т.е. по разным направлениям. Перечислим пять таких возможных направлений.
1. Компьютеры обретут "сознание", и возникнет сверхчеловеческий интеллект[2], как об этом уже более 40 лет твердят специалисты в области искусственного интеллекта (ИИ). Заметим, что в течение последних нескольких сот тысяч лет люди были умнейшими существами на планете. Весь наш социальный и технологический прогресс был создан человеческими мозгами.

2. Работы в области CAD, CAM, PDM, САПР и технической диагностики приведут к созданию самовоспроизводящихся машин.
3. Многие переборные (NP-полные) задачи будут решаться за полиномиальное время с использованием полиномиальных вычислительных ресурсов (этой проблеме и посвящён данный доклад).
4. Крупные компьютерные сети и их объединенные пользователи могут "осознать себя" как сверхчеловеческие разумные сущности.………………………………………………………………………………………………………………………
5. Машинно-человеческий интерфейс станет настолько тесным, что интеллект пользователей можно будет обоснованно считать сверхчеловеческим. Произойдёт интеграция человека с компьютерами.

С учётом тематики доклада здесь следует специально остановиться на метапроцедуре перебора[3] и переборных (NP-полных) задачах. При решении таких задач как раз и используется указанная метапроцедура. Первые квантовые алгоритмы (здесь примером может служить алгоритм факторизации П. Шора [2]) и появление первых КК показали, что новый тип компьютеров отлично справляются с процедурой перебора. И если вернуться к ис-тории науки, то в исследованиях в области кибернетики начала 70-х годов, связанных с ИИ, было замечено, что метапроцедура перебора является весьма «машинной», легко воплощаемой в программах. Именно поэтому она стала первой из метапроцедур, значение которой было осознано специ-алистами по имитации интеллектуальных процессов. Но, к сожалению, для многих из них в то время она так и осталась единственной и универсальной. Некоторые крайние сторонники перебора и поиска в дискретном лабиринте (лабиринте возможностей) так и говорили: «Когда ЭВМ станут еще более мощными, все задачи можно будет решать перебором, ибо перебор универсален».

Но тогда же, в начале 70-х годов американский математик С. Кук ввёл понятие NP-полных задач и доказал теорему, что для таких задач (в частности, для SAT-проблемы) время решения экспоненциально [3]. Эффективные алгоритмы для их решения в то время были не найдены. Такими NP-полными задачами являются почти все переборные задачи. Их решение с использованием классических компьютеров с одним процессором требовало экспоненциально большого времени. Это было доказано с использованием такой модели вычислений как классическая машины Тьюринга. Так как в то время эффективные алгоритмы для NP-полных задач не были найдены, то исследования по использованию метапроцедуры перебора относительно быстро увяли. Стали разрабатываться различные эвристические алгоритмы, в том числе генетические, муравьиные, жадные и др.

Поэтому возрождение интереса к процедурам и алгоритмам перебора с появлением КК часто рассматривается как возврат к прошлому, к этапу, уже пройденному наукой. Именно, поэтому новые научные идеи, новые научные истины, связанные с перебором, новые модели вычислений и новые квантовые алгоритмы перебора, возникающие в рамках квантовой революции (т.е. с появлением КК), порой встречают скрытое, но упорное сопротивление. Это объясняется тем, что они меняют стереотипы мышления, а также устоявшиеся парадигмы и не только в computer science (в частности в области САПР и технической диагностики), но и в тесно связанной в ней теорией управления (control science). С точки зрения науковедения и философии науки в этом нет ничего нового. Ещё в начале XX века Макс Планк утверждал: «Новые истины побеждают не так, что их противников убеждают, и они признают свою неправоту, но большею частию так, что противники эти постепенно вымириют, а подрастающее поколение усваивает истину сразу, со школьной скамьи».

Такое тихое подспудное сопротивление можно объяснить ещё и тем, что для последователей той или иной теории сомнения в её исходных принципах и моделях не уместны. Их историческая миссия заключается в том, что-бы развить теорию, вывести всевозможные следствия из основ, заложенных классиками. Поэтому нередко случается так, что адепты оказываются ортодоксальнее своих кумиров. Одним из таких кумиров для многих математиков и специалистов в области теории вычислений до сих пор остаётся английский математик А. Тьюринг. Он заложил основы абстрактной теории вычислений на базе классической универсальной машины Тьюринга. Здесь уместно напомнить о том, как и когда создавалась такая модель вычислений. Первое описание машины Тьюринга, которая является теоретическим аналогом многих классических компьютеров, было опубликовано в 1936 г. [4]. Следовательно, машина Тьюринга с её бесконечной бумажной лентой появилась на 9 лет ранее первого электронного компьютера ЭНИВАК (США, 1945 г.). Подчеркнём, что в то время (то есть в момент публикации описания машины Тьюринга) не существовало никаких однопроцессорных ЭВМ. В то время машина Тьюринга считалась физически нереализуемой, так как, по сути, эта машина с её бесконечной бумажной лентой является антропоморфной. И действительно эта машина была моделью вычислений, которые выполняет очень терпеливый, очень аккуратный, методичный и педантичный математик. Он имеет в своём распоряжении неограниченную по длине полосу (ленту) бумаги и неограниченное число карандашей. При этом математик, выполняя некоторую механическую процедуру записи, счи-тывания и движения по ленте, не использует свою интуицию, не использует знание и понимание математических зависимостей и закономерностей.

Однако абстрактная теория вычислений, основанная на машине Тьюринга, и сама классическая машина Тьюринга, в последнее время с появлением КК подвергается достаточно жёсткой критике. Так, один из пионеров квантового компьютеростроения Д. Дойч утверждает: «Теория вычислений традиционно изучалась абстрактно как раздел чистой математики. При этом теряется её суть. Компьютеры – это реальные физические объекты, а вычисления – это реальные физические процессы. Поэтому то, что может вычислить компьютер и то, что он вычислить не может определяется исключительно законами физики, а не чистой математикой». И далее в своей книге [5] Д. Дойч приводит просто убийственные фразы относительно Тьюринга и его машины: «Тьюринг надеялся, что его абстрактная бумажная модель настолько проста, настолько открыта, чётко определена и понятна, что не нуждается ни в каких допущениях относительно физики, без которых её можно было исказить постижимым образом. Следовательно, она может служить фундаментом абстрактной теории вычислений, независимо от физики, лежащей в её основе. «Он считал, ¾ как однажды насмешливо выразился Р. Фейнман, ¾ что он понял бумагу». Но он Тьюринг ошибался. Реальная квантовоме-ханическая бумага очень отличается от того абстрактного мате--риала, который использует машина Тьюринга». От себя добавим, что и квантовый параллелизм также радикально отличается от параллелизма многоленточных и многоголовочных модификаций машины Тьюринга.
Большим недостатком бумажной машины Тьюринга и всех её модификаций по сравнению с «квантовой бумагой», является то, что в одной клетке бумажной ленты машины Тьюринга можно записать только один символ. В одном разряде оперативной памяти (ОП) классического компьютера также можно записать только одно число: либо 0, либо 1. Число символов, которые можно записать в одной клетке «квантовой бумаги», больше любого наперед заданного числа . Другими словами в одном разряде квантового регистра КК можно записать символов и >.

Абстрактная теория вычислений в наше время, а также такая важная для инженерной практики часть этой теории как теория сложности вычислений, испытывают глубокий кризис. Чистая математика и её служители, опираясь на классическую машину Тьюринга, зашли в тупик: уже более сорока лет они не могут решить центральную проблему (ЦП) современной дискретной математики:

P = ? NP. (1)

В (1) P – это класс задач, для которых были найдены эффективные алгоритмы, решающих их за полиномиальное время на компьютерах с одним процессором. Символ NP в (1) обозначает класс задач, для которых такие алгоритмы не найдены. Время их решения является экспоненциально большим.

В настоящее время ЦП занимает первое место в списке задач третьего тысячелетия. В связи с этой проблемой уместно подчеркнуть следующий любопытный результат, полученный специалистами в области социологии науки. Им удалось опросить многих математиков. Выяснилось, что 80% математики убеждены в том, что P ¹ NP. Но при этом математики ¾ ревнители строгости выводов и утверждений ¾ доказать неравенство (P ¹ NP) не в состоянии. Другие математики (их 9%) считают, что P = NP, но и эти ригористы доказать равенство (P = NP) также не могут. Представители третьей группы математиков (их 9%) считают, что в рамках существующей парадигмы, основанной на классической машине Тьюринга, решить ЦП не возможно. Дело в том, что классическая машина Тьюринга является уточнением понятия «алгоритм», а всякое возможное уточнение алгорима, как утверждают математики из 3-ей группы, строго говоря, является сужением этого понятия. Однако предложить новую парадигму, т.е. новую реалистичную модель вычислений математики третьей группы оказались не в состоянии (ещё 2% математиков не определились с ответом).

Здесь целесообразно подчеркнуть, два момента. Было доказано (см.[6-9], что для решения ЦП необходимо построить алгоритм, который решал бы только одну задачу (например, SAT-проблему) из класса NP за полиномиальное время и с использованием полиномиального объёма памяти и полиномиального числа «процессоров», т.е. элементарных вычислительных модулей. Позднее, узнав об этой проблеме математики стали считать её подарком себе и математике от computer science. И второй момент: ЦП зародилась в обществе “инженеров”, т.е. учёных ¾ специалистов в области computer science и, по сути, вокруг ЦП сформировалась новая научная дисциплина — теория вычислительной сложности. Известный американский математик А. Вигдерсон в [10] утверждает «Не смотря на то, что эта дисциплина вообще и, в частности, ЦП приобрели выдающееся положение в пределах математического сообщества в течении последних десятилетий, ЦП до сих пор в значительной степени считается задачей computer science». Инженеры пытались и пытаются определить время вычисления массовых задач на каждом конкретном компьютере с помощью некоторого конкретного алгоритма или программы, реализующей этот алгоритм. При этом инженеры используют конечный и точный анализ.

Математики, используя более общие, по их мнению, асимптотические оценки для сложности вычислений на базе классической машины Тьюринга, быстро подмяли под себя инженеров и, оттеснив их, заняли лидирующие позиции в теории сложности. Использование асимптотических оценок математики объясняют тем, что асимптотическая точка зрения «стала неотъемлемой частью теории вычислительной сложности» [7]. Более того, некоторые математики считают, что конечный и точный анализ, который используют специалисты в области computer science, «затуманивает ту математическую структуру, которую выявляют асимптотические оценки сложности вычислений» (см. [10]). Использование же асимптотических оценок математики также оправдывали более общим теоретическим подходом. Использование классической машины Тьюринга математики обосновывали тем, что она является теоретическим аналогом любого классического компьютера с одним процессором. Тогда же в процессе конкуренции между математиками и инженерами и возникла дихотомия классов P и NP. Но неудачные попытки решить ЦП подорвали доверие и к математикам, и к их подходам к к решению ЦП на базе машины Тьюринга.

В середине 90-х годов на арене теории сложности вычислений и ЦП появилась «третья сила». Такой силой выступили физики, обосновавшие возможность построения КК, которые представляют собой качественно новый класс вычислителей. В связи с этим физик Дж. Прескил в 1998 г. утверждал [11]: «Результаты тридцатилетних исследований в области теории сложности вычислений так и останутся математическими истинами, как, например, теоремы, характеризующие возможности классических компьютеров. Но они не устоят как физические истины, так как классическая машина Тьюринга ¾ неподходящая модель для вычислений, которые реально могут быть выполнены в нашем физическом мире. Если квантовая теория сложности действительно отличается от классической ¾ как подозревается, но пока не доказано, ¾ то этот результат перевернёт основы computer science. В более отдалённой перспективе этот результат окажет сильное влияние на развитие компьютерных и других технологий».

Здесь уместно отметить и то, как нерешённость ЦП современной дискретной математики тормозит развитие не только computer science, и тесно связанной с ней дискретной математики, но и всей математики в целом. Этот факт очень удачно подметил А. Вигдерсон. Учитывая нерешённость ЦП, в 2006 г. он утверждал [10]: «Сегодня это сдерживает развитие многих направлений исследования математических структур в области алгебры, топологии, геометрии, анализа, логики, и более того сдерживает развитие даже таких направлений изучения структур, которые apriory кажутся никак не связанными с вычислениями. Эта вездесущность центральной проблемы превращает каждого математика против его воли в замаскированного потенциальной учёного в области computer science.» . Исходя из всего сказанного выше, можно утверждать, что решить ЦП на платформе классической машины Тьюринга не возможно. Решить ЦП можно только на платформе новой модели вычислений и эта модель должна быть моделью КК или КвУ.

1. КГТ и логические основания новой модели вычислений

Ранее в наших работах была предложена модель вычислений в виде идеального генератора тестов (ИГТ) для классических ускорителей, т.е. для классических проблемно-ориентированных процессоров [12-19]. Классический ИГТ и параллельно-последовательные D-алгоритмы позволяют решить ЦП относительно временной сложности, но при этом требуются экспоненциально большие объёмы ОП и экспоненциально большое число элементарных вычислительных модулей [12-16].

Здесь будет (рис. 1) приведена новая модель вычислений как идеальный квантовый генератор тестов (КГТ), который является естественный продолжением и развитием классического ИГТ.

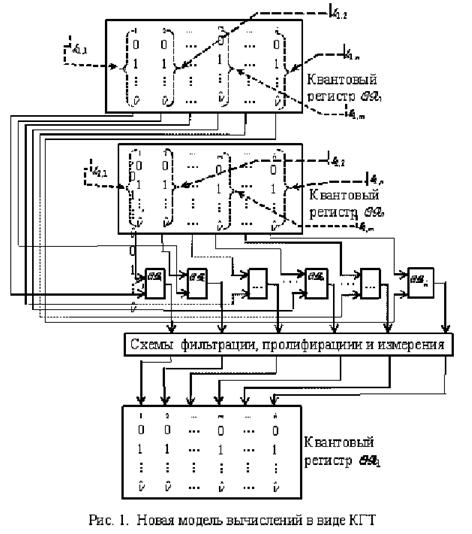
По сути, КГТ, представленный на рис.1 является проекцией или конкретизацией известной схемы идеального КК, приведённой в [20,21][4]. КГТ как и схема КК в [20,21] управляется классическим компьютером с помощью лазерных или СВЧ-импульсов (на рис. 1 классический компьютер не показан). Но в отличие от схемы идеального КК в [20,21], на рис. 1 показан модель КвУ в виде КГТ, содержащего два квантовых регистра[5]: QR₁ и QR₂, построенных не из кубитов, а из кунитов. Размерность гильбертова пространства для кубита: dim H = 2. Для кунита dim H = . Предполагается, что число кунитов в QR₁ и QR₂ одинаково и равно n. На рис. 1 куниты регистра QR₁ обозначаются k_1,m, а куниты QR₂ — k_2,m (m = ). Куниты QR₁ и QR₂ соединены с квантовыми блоками пересечений (блоками QB_m), реализующими элементарную операцию a_g пересечения. Операция a_g является основной операцией D-исчисления [23], и обычно задаётся таблицей (см. табл. 1). В табл. 1 c_j,q – значение в координате j куба C_q, с которым пересекается куб сокращённой или полной таблицы истинности. Символ q_j — обозначает значение в j-ой координате конкатенации K_r строк таблиц истинности логических элементов, относящихся к рангу r (см. далее).

Таблица 1

Правила выполнения операции ag = cj,q Ç xj
№	cj,q Ç qj,g	сj,(q+1)	№	cj,q Ç qj	с j,(q+1)	№	cj,q Ç qj	с j,(q+1)
1	0 Ç 0	0	4	1 Ç 0	Æ	7	~ Ç 0	0
2	0 Ç 1	Æ	5	1 Ç 1	1	8	~ Ç 1	1
3	0 Ç ~	0	6	1 Ç ~	1	9	~ Ç ~	~

В классическом ИГТ функция блока B_m описывается табл. 1, так как он реализует операцию a_g в виде комбинационного устройства (КУ). В КГТ блок QB_j (рис. 1), реализует квантовую эволюции, которая описывается унитарной матрицей R_j, матрицей Рота. Матрица R_j будет приведена далее. Схемы фильтрации, пролиферации и измерения реализуют отбраковку пустых кубов, перезапись вновь полученных кубов в соответствующий кунит k_1,m регистра QR₁ (операция пролиферации) и измерение квантового регистра в конце вычислений. Заметим, что на рис. 1 регистра QR₁ показан дважды.

Теперь можно привести в виде постулатов логические основы КГТ. Их можно также рассматривать как дополнение известных критериев Ди-Вин-ченцо [24]. Эти критерии определяют базовые требования к аппаратуре КК. Аппаратура КК, разработанная инженерами-физиками должны удовлетворять этим критериям.
Постулат 1. Для решения SAT-проблемы для заданного уравнения (т.е. для решения обратной задачи Ĭ) достаточно найти или построить хотя бы один вектор X_i - см.[6, 9].
Постулат 2. Квантовые разряды (кубиты, кутриты или куниты) и квантовые элементы рассматриваются как абстрактные математические объекты, с некоторыми заданными свойствами [25, стр. 33].

В данном случае состояния квантовых разрядов в качестве математических объектов описываются суперпозициями векторов состояния ¾ векторов . Для кунита суперпозиция вектора состояния имеет вид :

(2)

Для описания функционирование каждого квантового логического элемента (квантового вентиля) будет использована унитарная матрица U^†_k.
Постулат 3. Несмотря на то, что в n квантовых разрядах (кунитах) может храниться различных чисел, в процессе измерения («квантового считывания») мы можем получить только одно
n-разрядное число Ň. Какое конкретно число Ň будет получено из возможных чисел определяется амплитудами суперпозиции (2) для каждого квантового разряда — см. также постулат 4.
Постулат 4. В процессе измерения квантового регистра в разряде m некоторое число Ň будет получено с вероятностью .

Так, в случае кубита мы получаем либо результат 0 с вероятностью , либо результат 1 с вероятностью . Так, в случае кубитов образуется n-разрядное двоичное число Ň.
Постулат 5. Сумма квадратов модулей амплитуд для квантовых разрядов всегда равна единице.

В общем случае для кунитов:

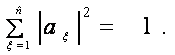⁽³⁾

Постулат 6. Любая унитарная матрица U^† описывает физически возможный квантовый элемент (квантовый вентиль) — см. [25, стр. 40].

Для постулата 6 можно привести и обратное в некотором смысле утверждение: матрица U_k , описывающая всякий квантовый элемент , должна быть унитарной: U_k = U^†_k. Постулат 6 является следствием постулата об эволюции [11, стр. 50; 25, стр. 116]. В настоящее время известно достаточно много квантовых элементов (вентилей), многие наборы которых образуют полный базис — см. [25, стр. 42-44]. Все унитарные матрицы рассматриваемых здесь вентилей U^† = являются квадратными и симметричными, а все матрицы многокубитовых элементов являются квадратными, разреженными и симметричными[6] . В качеств примеров можно назвать матрицы таких элементов, как матрица U^†_CN «управляемого инвертора» CNOT («сумма по модулю 2»), матрицы U^†_T (матрица элемента Тоффоли), U^†_Fr (матрица элемента Фредкина), а также матрица элемента обмена U^†_обмен – см. [25]. О физической реализации кубитов, кутритов и, в общем случае, кунитов здесь мы не говорим. Скажем лишь, что их можно реализовать на основе спинов[7] тех или иных квантовых частиц (например, фотонов или электронов).

В связи с тем, что при описании квантовых D-алгоритмов используются матрицы, классическое исчисление кубических комплексов, разработанное Дж. П. Ротом модифицируется в новое матричное D-исчисление. Основными отличиями нового исчисления, которые релевантны здесь применительно к случаю решения ЦП и, в частности, SAT-проблемы, являются следующие отличия.
1. Вместо таблиц истинности используются ортогональные[8] бинарные матрицы. Примером могут служить матрицы U^†_X, а также U^†_CN, U^†_T и U^†_Fr — см. [25].
2. Кодирование символов алфавита A (A = {0,1, ~, Æ})[9], который используется в классическом исчислении кубических комплексов многозначно. Правила в табл. 1 (см. выше) описывают выполнение операции a_g и эти правила однозначны. Теперь, опираясь на табл. 1, приведём таблицу правил многозначного кодирования символов алфавита A ¾ см. табл. 2. Из табл. 8 видно, что символ Æ закодирован двумя символами 01 и 10. Остальные символы A закодированы трёмя символами. Например, 0 Î A закодирован символами: 00, 02 и 20 (см. также табл. 1).

Таблица 2

Символ алфавита A	0	1	^~	^Æ
Двоичный код	00	01	10	11
Десятичный код	0	1	2	3
Двузначный десятичный код	00 (0 Ç 0=0) 02 (0 Ç ~= 0) 20 (~ Ç 0 = 0)	11 (1 Ç 1 = 1) 12 (1 Ç ~ = 1) 21 (~ Ç 1 = 1)	20 (~Ç0 =0) 21 (~Ç1 =1) 22 (~Ç~ = ~)	01 (0 Ç 1 =Æ) 10 (1 Ç 0 = Æ)

Такой способ кодирования связан с использованием обратимых матриц и, в частности, ортогональной перестановочной матрицы Рота ¾ матрицы R_j, реализующей в новом исчислении операцию a_g. Правила выполнения операции a_g приведены в табл. 1. Выше уже было упомянуто, что правила выполнения элементарной операции a_g пересечения в новом матричном исчислении описываются элементарной матрицей Рота ¾ матрицей U_R, названной в честь Дж. П. Рота.

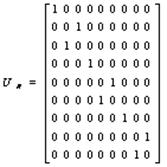(4)

Один из вариантов такой матрицы U_R показан выше ¾ см. (4). Подчеркнём, что в соответствии с постулатом 6 любая унитарная матрица U^† описывает физически возможный квантовый элемент.
Лемма 1 Матрица U_R является унитарной матрицей: U_R = U^†_R.
(В данном докладе доказательства не приводятся).

В случае использования кунитов для описания пересечения куба C_q и конкатенации K_r (C_q ÇK _r) необходимо использовать блочно-диагональные матрицы. Здесь нас, прежде всего, интересуют блочно-диагональные матрицы Рота ¾ U_RБ-Д,. Матрица U_RБ-Д, ¾ блочно-диагональная матрица Рота, в которой в качестве блока (подматрицы) используется матрица U^†_R = (l = =) ¾ см. (5).

U_{RБ-Д, =} . (6)

Теперь необходимо доказать, что матрица U_RБ-Д, (15) является унитарной.
Лемма 2. Блочно-диагональная матрица U_RБ-Д, является унитарной:

U_RБ-Д,= U^†_RБ-Д,. (7)

Постулат 7. Сложность и физический объём V интегрального квантового вентиля, реализующего блочно-диагональную матрицу A и выполняющего функцию f(x_1,1, x_{1, 2}, …, x_1,, x_2,1, x_{2, 2}, …, x_2, ) над двумя кортежами переменных, записанными в двух кунитах, может оставаться постоянным независимо от числа b подматриц-блоков в матрице A.

V = const. (8)

Продолжением данного доклада является доклад автора «Квантовые D-алгоритмы и центральная проблема современной дискретной математики».

Литература

1. В. Виндж. Технологическая сингулярность, Журнал «Компьютерра», 1 сентября 2004 г.

2. URL: http://old.computerra.ru/think/35636/

3. Shor P.W. Algorithms for quantum computation: discrete logarithms and factoring. / Proceeding 35^th Annual Symposium on Foundation of Computer Science. IEEE Press. Los Alamos. CA. 1996.

4. S. Cook. The complexity of theorem-proving procedures. / In Conference Record of Third Annual ACM Symposium on Theory of Computing, 1971, pp. 151–158.

5. Alan M. Turing. On Computable Numbers, with an Application to the Entscheidungsproblem. Proceedings of the London Mathematical Society, 42:230-265, 1936.

6. Д. Дойч Структура реальности. (The Fabric of Reality). — РХД. — Москва-Ижевск. — 2001. ISBN 5-93972-040-4

7. Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. М.: Мир, 1982. — 584 с.

8. Пападимитриу Х., Стайглиц К. Комбинаторная оптимизация. Алгоритмы и сложность. М.: Мир, 1985. ― 512 стр.

9. Harel Algorithmics: The Spirit of Computing Addison-Wesley, Reading, MA, 3rd edition (with Y. Feldman), 2004.

10. Крупский В.Н. Введение в сложность вычислений. М.: «Факториал пресс», 2006

11. Wigderson A. P. NP and mathematics – a computational complexity perspective. 2006. MIT Press and McGraw-Hill. P. 3-86.
URL:: http://www.math.ias.edu/~avi/PUBLICATIONS/MYPAPERS/W06/W06.pdf

12. Прескилл Дж. Квантовая информация и квантовые вычисления (Том I). Москва-Ижевск: ИКИ (НИЦ Регулярная и хаотическая динамика), 2008. — 464 стр.

13. Правильщиков П.А. Закон сохранения перебора и естественный параллелизм D-алгоритмов для построения тестов и моделирования в технической диагностике. // Автоматика и телемеханика. 2004. № 7. Стр. 156-199.

14. Правильщиков П.А. «Физическая» теорема Нётер в фотонике и computer science (Часть I). // Прикладная физика, 2005, № 6. С. 144-154.

15. Правильщиков П.А. «Физическая» теорема Нётер в фотонике и computer science (Часть II). // Прикладная физика, 2006, № 1. С. 95-109.

16. Правильщиков П.А. Идеальный генератор тестов и решение центральной проблемы современной дискретной математики. / Четвёртая Международная конференция по проблемам управления (26-30 января 2009 г.): Сборник трудов. М.: Учреждение Российской академии Институт проблем управления им. В.А. Трапезникова, 2009. — 2030 с. (с. 1487 - 1499). ISBN – 078-5-91450-026-6.

17. Правильщиков П.А. Фундаментальные проблемы управления и гипервычисления. / PACO-2010, Труды пятой международной конференции «Параллельные вычисления и проблемы управления». М.: Институт проблем управления РАН. 26-28 октября 2010. — 1235 с. (С. 709-757). ISBN 978-5-91450-064-8.

18. Правильщиков П.А. Квантовый параллелизм и квантовые D-алгорит-мы. /Труды шестой международной конференции «Параллельные вычисления и задачи управления PACO'2012». М.: ИПУ РАН, 2012. Том 3. Стр. 47-66. ISBN 978-5-91450-064-9 (т. 3).

19. Правильщиков П.А. Квантовый параллелизм и новая модель вычислений. / Труды 12-го Всероссийского совещания по проблемам управления ¾ ВСПУ-2014. М.: Институт проблем управления им. Трапезникова РАН. 2014. 9616 с. Стр. 7319-7334. ISBN 978-5-91450-151-5. № госрегистрации: 0321401153, 2014.

20. Правильщиков П.А. Квантовый параллелизм и решение уравнений в задачах управления на базе новой модели вычислений. / Труды 12-го Всероссийского совещания по проблемам управления ¾ ВСПУ-12.
М.: Институт проблем управления им. Трапезникова РАН. 2014. 9616 с. Стр. 7335-7351. ISBN 978-5-91450-151-5. № госрегистрации: 0321401153. 2014

21. Валиев К. А., Кокин А.А. Из итогов ХХ века: от кванта квантовым компьютерам (I. Физические основы и принципы построения квантового компьютера). // Известия вузов ЭЛЕКТРОНИКА, № 45, 2000. С. 46-52.

22. Валиев К. А., Кокин А.А. Квантовые компьютеры: надежды и реальность. ¾ Москва-Ижевск: НИЦ «Регулярная и хаотическая динамика», 2002, 320 стр. ISBN 5-93972-024-2

23. Богданов Ю.И., Кокин А.А., Лукичёв В.Ф., Орликовский А.А., Семенихин И.А., Чернявский А.Ю. Квантовая механика и развитие информационных технологий. / Труды МСКФ-2011

24. Roth J.P. Diagnosis of automata failures: a calculus and method // IBM Journal of Research and Development. 1966. № 7 (July). P. 18-32.

25. C. H. Bennett, D. P. DiVincenzo "Quantum computing: Towards an engineering era?". Nature. 1995, 377, 6548. P. 389-390.

26. Нильсен М., Чанг И. Квантовые вычисления и квантовая информация: Пер. с англ.— М.: Мир, 2006. — 824 с.

---

[1] Уже около 200 000 лет человечество выживало, несмотря на мощные извержения вулканов, падение астероидов и стихийные пандемии. Но срок нашего выживания может сократиться всего до нескольких десятилетий, если возобновить использование ядерного оружия. В связи с этим уместно упомянуть теорию Большого Фильтра. Эту теорию принято связывать с именем Э. Ферми, который впервые сформулировал парадокс, названный его именем. Существующая теория Большого Фильтра мешает многим исследователям с оптимизмом воспринимать новость о потенциальной населенности других планет. Парадокс Большого Фильтра, сформулированный Ферми, – это аргумент для учёных, который объясняет, почему до сих пор не найдена ни одна планета, населенная чем-либо или кем-либо, несмотря на наличие сотен миллиардов звездных систем в прилегающей к нашей Галактике области. Согласно теории Большого Фильтра, разумная жизнь либо крайне редка, либо имеет тенденцию к вымиранию. И как показывает В. Виндж [1], к вымиранию людей может привести не только ядерное оружие, но и технологическая сингулярность, в частности, создание сверхчеловеческого интеллекта.

[2] Формального и общепризнанного определения понятия «сверхчеловеческий интеллект» (иногда используют термин «искусственный суперинтеллект») не существует. Здесь сверхчеловеческий интеллект определяется как интеллект, который быстро и с успехом решает переборные задачи, которые человек (биологический компьютер) не может решить за время всей своей жиз-ни. Например, КК, используя квантовый алгоритм факторизации П. Шора [2], за 80 сек. взломает любой пароль наиболее распространённой современной системы защиты данных (RSA).

[3] Подчеркнём, что термин «метапроцедура перебора» ввёл один из основателей советской школы кибернетики М.Л. Цетлин.

[4] Необходимо подчеркнуть, что превосходные работы [20,21] опубликованы в 2000 и 2002. В них отражено состояние развития КК на то время. Более новый, но краткий обзор современного состояния и перспектив быстрого развития КК и КвУ приведён в [18]. См. также обзор в [22].

[5] На самом деле КГТ содержит один квантовый регистр, но условно все нечётные разряды относятся к регистру QR₁, чётные разряды – к регистру QR₂.

[6] Напомним, что симметричной (или симметрической) матрицей называют такую матрицу A, что ^.

[7] Напомним, что физическое понятие «спин» (от англ. spin – вертеться, крутиться) определяется как собственный момент импульса элементарных частиц, имеющий квантовую природу и не связанный с перемещением частицы как целого.

[8] Ортогональные матрицы являются частным случаем унитарных матриц.

[9] Алфавит A = {0,1, ~, Æ} является неполным алфавитом D-исчисления, но его вполне достаточно для решения SAT-проблемы.