An
approach is proposed for Steiner trees construction in the case of presence of
areas through which the objects connecting is prohibited. The approach is based
on a dynamic rebuilding of network connections without additional vertices by
adding branch points, and moving them to the optimal position using the
force-based algorithm.
При проектировании
коммуникаций (дорог, линий электропередач, трубопроводов, соединений на
печатной плате) возникает необходимость построения сети минимальной длины. В
теории графов известны эффективные (полиномиальные) алгоритмы Краскала и Прима
решения задачи построения минимального остовного дерева [1]. Однако в
большинстве случаев введение дополнительных вершин позволяет получить сеть
меньшей длины. Деревья с дополнительными вершинами называют деревьями Штейнера
[2]. В отличие от задачи построения минимального остовного дерева, для задачи
Штейнера (поиск деревьев Штейнера минимальной длины) не известны полиномиальные
по сложности методы решения [3 – 5].
В дереве Штейнера все
соединения должны быть отрезками, соединяющими вершины (терминальные и дополнительные).
В каждой дополнительной вершине должны сходиться три отрезка, а в терминальных
– не более трех. Угол между отрезками, сходящимися в одной точке, не должен
быть меньше 120°. Построить дерево Штейнера с выполнением перечисленных
достаточных условий нетрудно, но оно не обязательно будет минимальным (рис.1).
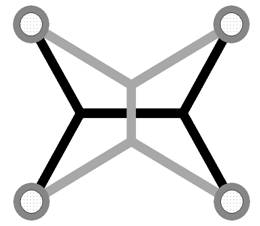
рис. 1.
Минимальное (черный цвет) и неминимальное (серый цвет) деревья Штейнера
Если четыре терминальных
вершины образуют выпуклый четырехугольник,
критерий минимальности прост: пары терминальных вершин, соединенные с дополнительной
вершиной, должны быть расположены напротив острых углов, образованных
диагоналями четырехугольника [2]. Если диагонали ортогональны, оба дерева имеют
одинаковую длину.
При проектировании реальных
коммуникаций необходимо учитывать наличие различного рода препятствий, что, к
сожалению, ограничивает возможность использования как алгоритмов построения минимального
остовного дерева (рис. 2а), так и геометрических
методов построения деревьев Штейнера (рис. 2б).
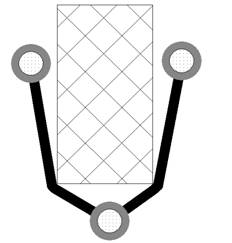

а) б)
рис. 2.
Минимальные сети при наличии препятствий
В работе предлагается
подход к построению деревьев Штейнера при наличии препятствий, основанный на
динамическом перестроении сети соединений, не содержащей дополнительных вершин.
Основные механизмы: создание дополнительных вершин и итерационное перемещение
их в точку равновесия с использованием силового алгоритма.
Пусть получена сеть
соединений, не содержащая дополнительных вершин. На реальных сетях пары
терминальных вершин не всегда соединяются отрезком прямой. На пути соединения
могут быть препятствия различной природы. Если соединение пары вершин содержит
более одного отрезка (рис. 2б), в качестве виртуальной
терминальной вершины следует использовать конец отрезка, инцидентного вершине.
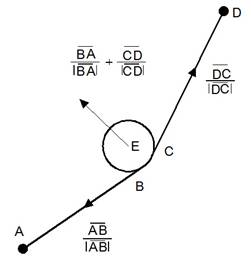
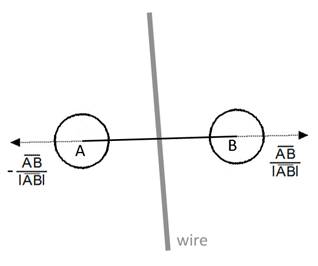
Силовое размещение
Огибая элементы топологии,
проводник оказывает на них «давление», как бы «выталкивая» со своего пути (рис.
3а). Это давление направлено к центру окружности и численно равно отношению
уменьшения длины проводника к величине сдвига элемента в сторону давления (с
необходимым коэффициентом, если стоимость длины для разных проводников различна).
Точно так же проводник «тянет» элементы, к которым прикреплён концами. Одновременно
с этим проводник «расталкивает» элементы топологии, между которыми он проходит
(рис. 3б).
Суммарная сила, приложенная
к элементу (компоненту, межслойному переходу, точке ветвления проводников)
всеми проводниками, определяет, в какую сторону «желает» сдвинуться элемент и
как сильно.
|
|
|
|
а) |
б) |
|
рис. 3. Действие сил на
элементы топологии |
|
Перемещение
осуществляется с уменьшением шага на каждой итерации.
Локальная оптимизация
Наличие угла, меньшего 120°
(рис. 4а и 4в), между парой сегментов, инцидентных одной вершине (терминальной
или дополнительной), – признак локальной неоптимальности подсети. В этом случае
следует добавить дополнительную вершину: пара сегментов заменяется на три
сегмента, инцидентных дополнительной вершине (рис. 4б и 4г). Положение
дополнительных вершин оптимизируется с использованием силового алгоритма (рис. 4в
и 4д).
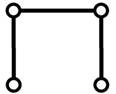
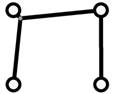
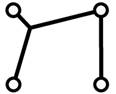
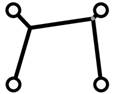

а) б) в) г) д)
рис. 4.
Перестроение сети соединений
Если добавленная вершина
оказалась смежной с другой добавленной, следует проверить минимальность четырёхконтактной
сети.
Если четырёхконтактная сеть
не минимальна (рис. 5а):
·
выбрать пару “диагональных” (принадлежащих диагонали четырехугольника)
терминальных либо виртуальных терминальных вершин;
·
отрезок, соединяющий терминальную (виртуальную терминальную) вершину с
ближней к ней добавленной вершиной, заменить отрезком, соединяющим терминальную
(виртуальную терминальную) вершину с дальней добавленной (рис. 5б);
·
положение дополнительных вершин оптимизировать с использованием силового
алгоритма (рис. 5в).
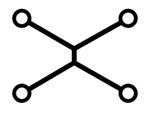
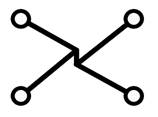
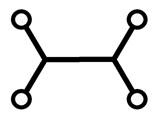
а) б)
в)
рис. 5.
Перестроение дерева Штейнера
Порядок
применения локальных процедур
Самое простое решение – «жадная» стратегия:
· углы между парами смежных
сегментов, инцидентных одной вершине, упорядочить в порядке возрастания;
· на каждой итерации выбрать
очередную пару сегментов, инцидентных одной вершине, с минимальным углом между
ними, и добавить дополнительную вершину, которую установить в оптимальную точку
с использованием силового алгоритма;
· если очередной угол больше
или равен 120° или все углы обработаны, закончить перестроение сети.
Достоинство: для углов, не имеющих общих лучей
(сегментов), добавление дополнительных вершин можно осуществлять параллельно и
экономить на вызовах процедуры, реализующей перемещение с использованием силового
алгоритма.
Однако у «жадной» стратегии можно отметить, по
крайней мере, три недостатка:
1.
Добавление дополнительных вершин сопровождается добавлением сегментов (и
углов между ними), что влечет изменение порядка после каждого добавления дополнительной вершины.
2.
Лучшие результаты можно получить, если рассматривать только вершины,
смежные с вершинами уже оптимизированной части сети, постепенно наращивая
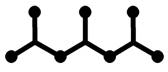
оптимизированную часть. Так, на рис. 6а все углы между сегментами равны 60°.
Если начать перестроение с первой слева верхней вершины, угол между сегментом,
соединяющим добавленную вершину со второй слева нижней вершиной, будет равен
90°. Поскольку угол меньше 120°, можно
продолжить перестроение, в результате будет получена кратчайшая по длине сеть
(рис. 6б). Следование «жадной» стратегии дает неоптимальную сеть (рис. 6в).

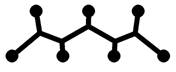
а)
б) в)
рис. 6. Перестроение
сети (а) постепенным наращиванием оптимизированной части (б) и с использованием
«жадной» стратегии (в)
3.
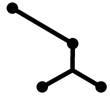
Рассмотрим фрагмент сети на рис. 7а. Сегменты,
инцидентные центральной вершине образуют углы 90° и 60°. Если начать
перестроение с угла 60°, будет получена неоптимальная сеть, при этом все
остальные углы – 120°, и дальнейшее перестроение невозможно (рис. 7б).
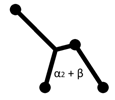
Если начать перестроение с угла 90° (рис. 7в), то перестроение можно
продолжить и получить сеть с меньшей длиной (рис. 7г).
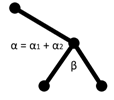
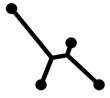
а)
б) в) г)
рис.7. Перестроение подсети
типа «звезда»
Таким образом, если два
смежных угла α и β в сумме образуют угол меньше 180°, то следует
начинать:
1.
C большего из смежных углов,
если в результате его деления отрезком до дополнительной вершины на углы α1
и α2 сумма α2 + β будет меньше 120°
(тогда можно будет добавить дополнительную вершину и для угла α2 + β)
(рис. 7в).
2.
Иначе, с меньшего из смежных углов.
Построение дерева Штейнера
начинается от некоторой (произвольной) висячей вершины. В любой момент работы
алгоритма существует оптимизированное дерево (Штейнера) для части вершин и
просто кратчайшее дерево для остальных вершин. Соответственно, есть множество
вершин (и ребер), уже включенных в оптимизированное дерево, есть множество
вершин (и ребер), не включенных в оптимизированное дерево, и множество пограничных
вершин (вершин фронта), в том числе дополнительных, для которых только часть инцидентных им
ребер включена в оптимизированное дерево.
Предложенный подход
реализован в САПР TopoR. Он не гарантирует построение минимальной сети, но,
в отличие от других подходов, позволяет при минимальных временных затратах
минимизировать длину сети с произвольным числом терминальных вершин, при этом
учитываются области, в которых прокладка соединений запрещена.
1.
Томас Х. Кормен [и др.] Алгоритмы: построение и анализ, 2-е изд. // М.: Издательский дом “Вильямс”,
2005. – 1296 с.
4. Z. A. Melzak, On the problem of Steiner // Canadian
Mathematics Bulletin, 1961. - №4. – pp. 143-149.
5. E. J. Cockayne, On the efficiency of the algorithm for Steiner
minimal trees // SIAM J.Appl. Math., 18 (1970), pp.150 –159.