Статистическая обработка измерительной информации в системах управления при наличии

сильной дискретизации наблюдений

Д.А. Мастеренко,
дир. центра. разр. средст. измер., к.т.н., metrologycenter@gmail.com,
ГИЦ МГТУ «Станкин», г. Москва

Вводится понятие сильно дискретизованных (по уровню) наблюдений. Обосновывается неадекватность методов статистического оценивания, основанных на модели непрерывных случайных величин, для ситуаций сильной дискретизации наблюдений. Приводятся статистические оценки измеряемых величин, которые могут быть интерпретированы как параметры линейной статистической модели, для сильно дискретизованных наблюдений. Предложены рекуррентная и робастная модификации процедуры оценивания для условий оценивания в реальном времени.

The concept of strongly discretized (by level) observations is formulated. Inadequacy of the statistical methods, based on the model of continuous random variables, in the case of strong observation discretization is shown. Statistical estimates of the measured values, which could be interpreted as the parameters of the linear statistic model, are given for the case of strongly discretized observations. Recursive and robust modifications of the estimating procedure are proposed for the real-time applications.

1. Задача оценивания измеряемых величин по сильно дискретизованным наблюдениям

Всё большее количество измерений в современном производстве выполняется автоматически или автоматизировано, с использованием электронных средств измерений и цифровых вычислительных устройств, в которых значения наблюдаемых физических величин представляются дискретным кодом. В связи с этим особое значение приобретает такая характеристика измерений, как дискретность, которая в той или иной мере присутствует в измерениях всегда, в виде или цены деления шкалы стрелочного прибора, или значения разряда аналого-цифрового преобразователя электронного средства измерения.

Здесь речь идёт о дискретизации наблюдений, которая в теории сигналов трактуется как квантование по уровню. В метрологической литературе широко используются термины «дискретность отсчета», «цена деления», которые относятся к дискретности по уровню измеряемой величины. Таким образом, в данном докладе под дискретизованными наблюдениями понимаются наблюдения значений физической величины средством измерения (СИ), дающим определенную дискретизацию по уровню.

В ряде практически важных ситуаций случайный разброс наблюдаемых величин оказывается соизмерим с дискретой («ценой деления») средства измерения – в терминологии настоящей работы, наблюдения являются сильно дискретизованными. Это связано с тем, что в настоящее время с развитием требований к качеству технологических процессов в машиностроении, приборостроении и других областях возникает противоречие: с одной стороны, повышение точности требует уменьшения дискретности, с другой – происходит повышение случайной составляющей относительно полезного сигнала.

Во многих ситуациях дальнейшее уменьшение дискретности либо невозможно из-за достижения технологических пределов, либо слишком затратно с экономической точки зрения. С другой стороны, исключить или существенно снизить случайную составляющую при проведении измерений в реальных условиях также либо невозможно, либо экономически затратно. Возникает противоречие, которое приводит к ограничениям точности измерений в ситуациях, когда случайный разброс наблюдений соизмерим с дискретой средства измерения, то есть при сильно дискретизованных наблюдениях.

Статистические методы обработки таких наблюдений в настоящее время не распространены в метрологической практике, в частности, не регламентируются существующими стандартами. Применение оценок, основанных на модели непрерывных случайных величин, к сильно дискретизованным наблюдениям приводит к погрешности оценивания, которая может быть снижена, если учитывать их дискретный характер. В частности, оптимальные в классической ситуации оценки наименьших квадратов или выборочного среднего, будучи применены к сильно дискретизованным наблюдениям, обладают смещением, не стремящимся к нулю с ростом объема выборки, то есть перестают быть состоятельными [1].

Очевидно, при дискретизации наблюдений происходит потеря информации. Более интересно, что, как показано в работе [2], количество потерянной информации можно снизить, если интерпретировать полученные значения наблюдений не как числа, а как события попадания истинных, реально недоступных, значений в соответствующие интервалы – дискреты средства измерения.

Таким образом, возникает задача поиска оценок параметров распределения наблюдаемых непрерывных величин в ситуациях, когда для наблюдения доступны не сами их значения, а лишь события попадания этих значений в известные интервалы.

2. Математическая модель наблюдений

Рассмотрим следующую модель наблюдений, охватывающую самые разные ситуации измерений при аддитивной случайной составляющей:

, (1)

где – значения выходного сигнала до дискретизатора (шкалы или аналого-цифрового преобразователя) при –м наблюдении; – совокупность измеряемых величин; – векторы управляемых величин (факторов); – некоторая функция, зависящая от факторов эксперимента и измеряемых величин; – параметр масштаба, который может быть известен или нет; – центрированные случайные величины, функция распределения которых считается известной; – количество наблюдений.

Прямым измерениям соответствует частный случай модели (1) при и , так что

(2)

и измеряемая величина служит для распределения наблюдений параметром сдвига.

Другим важным частным случаем является линейная статистическая модель:

. (3)

Линейность здесь понимается в смысле зависимости от параметра, тогда как зависимость от факторов может быть самой различной, например, в виде степенного или тригонометрического полинома. Очевидно, модель (2) является также частным случаем (3).

Вследствие дискретизации наблюдению доступны не значения величин , , а значения других – дискретизованных – величин , принадлежащие конечному множеству отсчетов «шкалы» с ценой деления и образованных по правилу

,

где означает интервал дискретизации, соответствующий отсчету шкалы . При дискретизации «с округлением» этот интервал (вернее, полуинтервал) определяется следующим образом:

,

а при дискретизации «с отсечением», что более соответствует аналого-цифровым преобразованиям,

.

Будем говорить, что наблюдения сильно дискретизованы, если число отсчетов , в которые укладывается вся выборка, невелико (2 – 4).

Распределение вероятностей дискретизованных наблюдений, очевидно, порождается распределением случайной части модели (1) и зависит от параметров – измеряемых величин, а также факторов:

.

В частности, при дискретизации с округлением

.

Далее будем предполагать случайные слагаемые в (1) – (3) независимыми, тогда совместное распределение дискретизованных наблюдений запишется следующим образом:

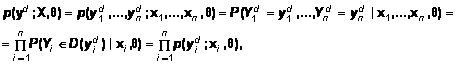(4)

где – вектор значений дискретизованных наблюдений, – матрица, состоящая, как из строк, из векторов факторов .

Проще всего предложить модификацию оценок максимального правдоподобия, учитывающую дискретизацию наблюдений. Для этого требуется найти максимум (4) по , то есть, с учетом введенных обозначений,

(5)

Такая оценка уже будет асимптотически несмещённой для широкого класса распределений.

3. Оптимальные оценки

Более важным, чем асимптотическая несмещённость, свойством оценок является оптимальность в некотором смысле.

Для постановки задачи о поиске оптимальной оценки обычно задают некоторую функцию потерь , возрастающую при удалении оценки от истинного значения параметра , и ищут оценку как функцию наблюдений (статистику) , минимизирующую математическое ожидание потерь

,

желательно, при любом значении .

Однако найти оценку, обеспечивающую такой минимум при всех значениях параметра, в рассматриваемой модели невозможно. Например, если в модели (2) истинное значение совпадает с серединой деления шкалы, то распределение дискретизованных наблюдений симметрично относительно , выборочное среднее не смещено, а его дисперсия быстро убывает, так что в этой точке улучшить оценку в смысле среднего квадрата погрешности уже нельзя.

Поэтому остается искать оценки, оптимальные «в среднем» по некоторому множеству значений параметра:

Для модели прямых измерений (2) естественно взять квадратичную функцию потерь , и оптимальная в этом смысле оценка будем иметь вид [3]

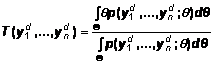(6)

Для линейной модели (3) и функции потерь в виде среднего квадрата погрешности оценивания (воспроизведения зависимости)

оптимальная оценка совершенно аналогична (6) [4]:

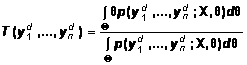, (7)

различие заключается в кратности интегрирования.

Нетрудно заметить сходство выражений (6), (7) с выражениями для оценок Питмена [5]. По этой причине предложено называть данные оценки «оценками типа Питмена».

Выше предполагалось, что параметр масштаба случайной составляющей известен. В [8] предложен способ оценить неизвестный параметр масштаба наряду с параметром и показано, что, в общем, вид оценок типа Питмена при этом остается тем же.

4. Оценивание в реальном времени при возрастающем объеме выборки

Оценки типа Питмена в виде (6), (7) обладают тем недостатком, что их вычислительная сложность значительно растет с увеличением числа наблюдений. Так, в ходе теоретического и экспериментального исследования оценок, описанного в главах 2 и 3, замечено, что вычисление оценок типа Питмена параметров линейной функции при объеме выборки занимает примерно в 5,5 раз больше времени, чем при объеме выборки .

Кроме того, во многих ситуациях данные поступают последовательно, так что их объем постоянно нарастает, и с каждым новым наблюдением требуется производить новое вычисление оценки.

Всё это делает желательным наличие рекуррентных (рекурсивных) процедур оценивания, позволяющих не хранить весь накопленный объем данных, а вычислять новое значение оценки после получения очередного наблюдения на основе предыдущего её значения и только последнего (или нескольких последних) наблюдений.

Обратим внимание на то, что оценки (6), (7) можно считать частным случаем байесовских оценок

, (8)

где апостериорная плотность распределения параметра получается из априорной по теореме Байеса в виде

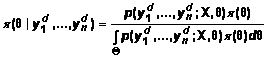. (9)

Если априорная плотность распределения равномерна на , то (9) и (8) равносильны (7).

Введём обозначения

Несложными преобразованиями из (9) можно получить, что

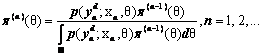(10)

Если теперь положить на , то (10) представляет собой рекуррентное соотношение для вспомогательных функций (которые уже можно и не рассматривать в качестве плотностей распределения), позволяющих вычислять оценки типа Питмена аналогично (8).

С практической точки зрения вместо того, чтобы производить интегрирование согласно (10), целесообразно выбрать конечное множество и интегрирование заменить суммированием:

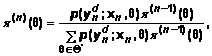(11)

(12)

Чтобы получить рекуррентные оценки, защищенные от влияния резко выделяющихся наблюдений (выбросов), то есть робастные [8-11], используем следующий прием. Будем использовать в формуле (11), начиная с некоторого значения , вместо нового дискретизованного наблюдения псевдонаблюдение , образованное по следующему правилу: если расстояние между прогнозом и ближайшей к нему границей интервала не превосходит (– настроечный параметр алгоритма), то ; иначе значение сдвигается в направлении на минимальное количество дискрет, при котором расстояние между и не превосходит . Иначе говоря, задаются два уровня отсечения: верхний и нижний:

, ,

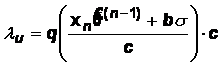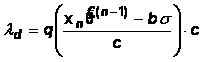( означает приведение к целому числу в соответствии с принятым в СИ способом – с округлением или с усечением), и принимается

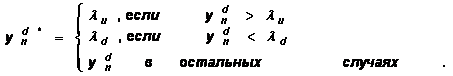
Для такой робастной рекурсии требуется иметь достаточно хорошую начальную оценку параметра. Её можно получить, например, вычислив оценку без робастных свойств на основе нескольких первых наблюдений, которые тщательно проверены на отсутствие выбросов.

Литература

1. Мастеренко Д.А. Статистическое оценивание результатов наблюдений с учетом их дискретизации по уровню//Измерительная техника. 2008. №7. С.11 – 15.

2. Мастеренко Д.А. Информационный аспект статистической обработки сильно дискретизованных наблюдений (байесовский подход)//Вестник МГТУ «Станкин». 2011. № 3. С.150-155.

3. Мастеренко Д.А. Выбор наилучшей оценки измеряемой величины по сильно дискретизованным наблюдениям//Измерительная техника. 2011. № 7. С.17-20.

4. Мастеренко Д.А. О подходах к оцениванию параметров по сильно дискретизованным наблюдениям//Вестник МГТУ «Станкин». 2010. № 3. С.88-94.

5. Боровков А. А. Математическая статистика.//М.: Лань, 2010 – 704 с.

6. Мастеренко Д.А. Исследование оценок измеряемой величины по сильно дискретизованным наблюдениям//Измерительная техника. 2011. № 8. С.22-24.

7. Мастеренко Д.А. Исследование оценок параметров линейной статистической модели по сильно дискретизованным наблюдениям //Вестник МГТУ «Станкин». 2010. № 3.

8. Хьюбер П. Робастность в статистике. - М.: Мир, 1984.

9. Фомин В.Н. Рекуррентное оценивание и адаптивная фильтрация//М.: Наука, 1984.

10. Хампель Ф., Рончетти Э., Рауссеу П., Штаэль В. Робастность в статистике. Подход на основе функций влияния/Пер. с англ.; под ред. В.М. Золотарева // М.: Мир, 1989.

11. Мастеренко Д.А. Повышение эффективности обработки измерительной информации в системах статистического управления процессами в машиностроении на основе рекуррентного робастного оценивания. Автореферат диссертации на соискание ученой степени кандидата технических наук//М.: МГТУ «Станкин», 1997.