Технология совмещения точечных множеств и поверхностей при контроле геометрии

крупногабаритных изделий

Е.В. Попов,
 препод. каф. НГМГ, д.т.н., проф., popov@sandy.ru
С.И. Ротков,
 зав. каф. НГМГ, д.т.н., проф., rotkov@nngasu.ru

А.А. Самойлов,
 аспир. каф. НГМГ, greatlimit@rambler.ru
ННГАСУ, г. Нижний Новгород

Аннотация

В данной статье предлагается способ численного решения задачи о совмещении заданного точечного множества и заданной поверхности в трёхмерном пространстве. Представлены результаты тестирования компьютерной программы, реализующей предложенный способ, на примере конкретных задач. Рассмотрены способы практического применения разработанного способа.

 

Abstract

The approach of numerical solution for the problem of fitting in 3-D of a given set of points and a given continuous surface is proposed in this paper. The results of testing the software which the proposed approach was implemented in on the concrete tasks were illustrated. The ways of practical application of the approach were considered.

Введение

В настоящее время многие отрасли промышленного производства нуждаются в автоматизированном контроле геометрии изделий. Процедура контроля геометрии изделий предполагает выполнение следующих этапов: измерение координат точек объекта, построение цифровой 3-D модели по измеренным данным, совмещение этой 3-D модели с 3-D моделью эталонного образца. Каждый из этих этапов может быть в разной степени автоматизирован. Для автоматизации 1-го и 2-го этапов на передовых отраслях промышленности используются измерительные системы, способные выполнять снятие координат точек изделия методами бесконтактного сканирования, передавать их на переносной ПК и строить по измеренным данным цифровую 3-D модель изделия.

3-й этап контроля геометрии реализуется в подобных системах, как правило, следующим образом. Предполагается, что существует ряд опорных точек, отмечаемых пользователем на эталонной модели изделия и на модели, полученной экспериментально. Измерительная система привязывает две модели к общей системе координат, исходя из знания опорных точек.

Для большинства предприятий подход, основанный на задании опорных точек, вполне приемлем (если опорные точки заданы на достаточно большом расстоянии друг от друга, то точность совмещения является достаточно высокой). Однако в ряде случаев такой подход не дает удовлетворительных результатов, например;

1.    Деформируемые изделия. Примером этих изделий являются стержневые крупногабаритные конструкции, способные прогибаться под собственной тяжестью. При каждом положении изделия в пространстве оно имеет разную форму. Поскольку эталонная модель изделия, заданная производственными нормативами, почти всегда является статической (задана лишь геометрическая, но не упругопластическая модель изделия), то жёсткая привязка в этом случае невозможна.

2.    Разборные и транспортируемые конструкции. Есть примеры перевозимых изделий, которые после каждой новой сборки нуждаются в проверке геометрической формы вне предприятия, на котором изделие было  однажды изготовлено.

3.    Проверка на соответствие формы поверхности изделия заданному математическому закону. Существуют изделия (например, зеркала больших телескопов, спутниковые и радиолокационные антенны), для которых требуется определить, насколько их форма отличается от параболической, сферической формы или формы, заданной другим аналитическим уравнением.

4.    Вычисление деформаций изделий. В некоторых исследовательских лабораториях при испытаниях материала его образцы подвергаются различным видам деформации. Иногда возникает задача вычислить перемещения определённых точек образца до и после нагружения. Имеется две различные структуры материала, которые необходимо совместить в одной системе координат, то есть найти точку и вектор привязки.

Таким образом, есть множество типов изделий, для которых является актуальной задача о совмещении в одной системе координат двух моделей объекта при условии отсутствия информации об опорных точках. При этом вышеперечисленные случаи относятся в основном к крупногабаритным типам изделий (с линейными размерами более 5-10 м).

Задача состоит в поиске оптимального взаиморасположения в трёхмерном пространстве двух множеств, при котором расстояние между этими множествами по некоторой заданной норме минимально. Каждое из двух множеств может быть либо точечным множеством, либо непрерывной поверхностью, либо кусочно-непрерывной поверхностью, либо произвольным множеством.

В настоящей статье предлагается алгоритм численного решения задачи для случая, когда первое множество является точечным, а второе множество – непрерывной поверхностью.

1. Постановка задачи и схема решения

Задача. Дано два множества – поверхность , параметрически заданная уравнениями   в параллелепипеде , и нумерованный набор точек ,  Требуется из всевозможных трёхмерных преобразований движения  найти такое преобразование , чтобы множество  являлось ближайшим к поверхности  по некоторой норме, то есть , где - функция расстояния от точки  до кривой  в евклидовом пространстве.

Рассмотрим следующую схему численного решения поставленной задачи (см. рис. 1).

1.    Осуществляется поиск 4-х точек из множества , образующих тетраэдр с наибольшим периметром среди всех других тетраэдров, построенных на 4-х различных точках множества .

2.    Организуется перебор с некоторыми заданными шагами  по параметрам . Для каждого из вариантов на поверхности отмечается точка  , где

3.    Для каждой из отмеченных точек  производится поиск всех линий пересечения  двух фигур – поверхности  и сферы с центром в точке  радиуса .

4.    Осуществляется обход каждой из найденных линий пересечения . На кривой отмечаются идущие друг за другом точки через заданное расстояние . Обозначим  каждую из точек .

5.    Для каждой из пар  осуществляется поиск всех таких точек  на поверхности , что .

6.    Для каждой из троек   вычисляется единственная точка ,  такая, что, во-первых, тетраэдры  и  равны, и во-вторых, тетраэдры  и  могут быть отображены друг в друга преобразованием движения в пространстве (исключается случай преобразования симметрии).

7.    Осуществляется проверка на близость точки  к поверхности . Если расстояние от точки  до поверхности  не больше заданного параметра , то осуществляется поиск 6 параметров  преобразования движения, переводящего точки  соответственно в точки  ( - вектор сдвига,  - углы поворота вокруг осей координат  соответственно). Каждая шестёрка параметров сохраняется в памяти. Совокупность всех таких найденных вариантов представляет собой набор решений задачи в первом приближении.

8.    Организуется итерационный процесс уточнения приближённых решений. На каждом -шаге итерационного процесса к имеющимся точкам (на 1-м шаге имеется 4 точки ) добавляется  точек из множества  по некоторому правилу. Затем производится варьирование определённым образом положений каждой из рассматриваемых в данный момент точек  в своих -окрестностях с заданным шагом  так, что исходный тетраэдр  и перемещённый тетраэдр  равны . Для каждой из рассматриваемых вариаций вычисляются параметры трёхмерного преобразования движения, переводящего точки  соответственно в точки , а затем - положения, в которые отобразятся этим преобразованием добавленные точки из множества . Если образы всех добавленных точек также отстоят от поверхности  не далее, чем на расстояние , то параметры преобразование запоминаются в список множества решений -го приближения. При этом . В качестве критерия останова может быть взято число выполненных итераций, либо достижение параметром  заданного наименьшего значения . (Правила добавления новых точек, сужения интервала ,, и варьирования положений точек, а также все выкладки в координатах не могут быть описаны в данной статье ввиду ограничения на её размер).

Описанный здесь способ решения был получен обобщением аналогичной задачи для двумерного случая. Более детальное описание решения двумерной задачи и обобщения её на трёхмерный случай можно найти в [1]. С момента публикации [1] авторами был изменён и доработан способ решения трёхмерной задачи. В частности, количество точек фигуры с наибольшим периметром и правила добавления новых точек изменились по сравнению с  [1].

2. Реализация численного решения в виде компьютерной программы

 

На основе описанного способа был разработан программный модуль “3DAnalyzer”, предназначенный для решения задачи совмещения точечного множества и поверхности . Входными данными модуля являются

·         файл с координатами точек множества

·         функция, задающая поверхность (задаётся внутри программного кода)

·         параметры алгоритма (шаги , , расстояние , точность , и др. параметры, от которых зависит точность и скорость алгоритма)

Выходные данные – массив различных  наборов ,  соответствующих трёхмерным преобразованиям движения, отображающих точечное множество  в положения, достаточно близкие к поверхности . В подавляющем большинстве случаев на практике рассматриваемая задача о совмещении имеет единственное решение, но модуль  “3DAnalyzer” способен в общем случае находить несколько решений задачи. При этом среди каждой группы решений, достаточно близких друг к другу (которые, как правило, соответствуют на практике одному решению), автоматически выбирается одно, наиболее точно удовлетворяющее условию задачи. Параметр, определяющий близость решений друг к другу, также является входным параметром модуля. Модуль в данный момент не применяется для обработки данных по следующим типам поверхностей:

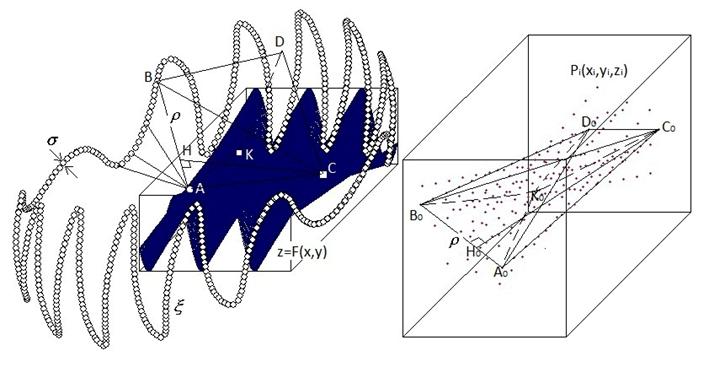
рис. 1  “Схема численного решения задачи”

 

Рисунок 1 был получен при помощи визуализации отдельной стадии работы модуля для поверхности .

3. Применение технологии совмещения поверхности и точечного множества при контроле геометрии изделий

Программный модуль “3DAnalyzer” в свою очередь является основой для программы для контроля геометрии изделий. Основная программа работает по следующим принципам. Входными данными для программы являются два точечных множества. Первое точечное множество – точки эталонной модели изделия (задаются согласно производственным нормативам), второе точечное множество – точки, полученные экспериментально (бесконтактным измерением). По измеренным точкам строится интерполяционная поверхность, которая подаётся на вход в модуль “3DAnalyzer” в совокупности с точками эталонной модели изделия. Затем среди всех решений, полученных при помощи модуля “3DAnalyzer”, выбирается одно (если пользователем не выбрана опция поиска многих решений) , наиболее точно удовлетворяющее условию задачи, после чего эталонная и экспериментальная модели изделия оказываются совмещёнными в одной системе координат. Это позволяет выполнить расчёт отклонений геометрии изделия в ряде заданных контрольных точек. Информация об отклонениях изображается графически и в цветовой гамме. Графики эталонной, экспериментальной моделей и отклонения геометрии могут быть экспортированы в файлы формата, совместимого с MS Excel и файлы формата графического редактора “K3 Freeware”, что полезно пир создании отчёта о состоянии изделия. Схема работы и интерфейс программы более подробно описаны в [2].

На рис. 2 показан пример работы модуля на данных, полученных экспериментально. Справа на рисунке изображены точки эталонной модели и тетраэдр наибольшего периметра, слева – те же точки, наложенные на интерполяционную поверхность согласно найденному решению задачи.

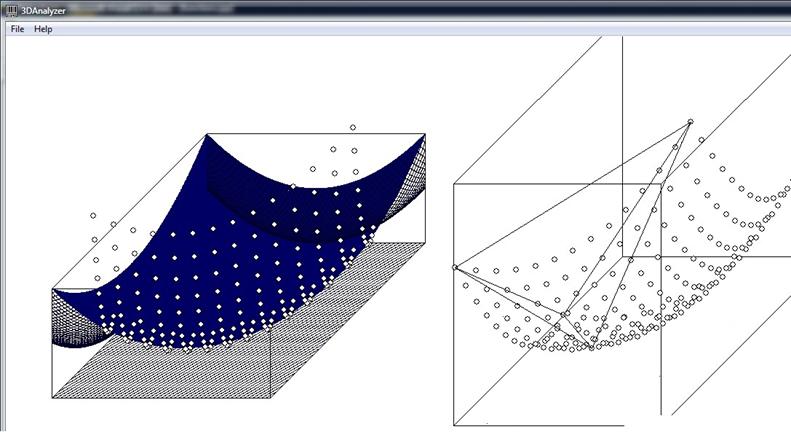
рис. 2  “Применение модуля 3DAnalyzer на экспериментально полученных данных”

Заключение

Предложен способ численного решения задачи о совмещении точечного множества и поверхности в трёхмерном пространстве. Способ реализован в виде программного модуля “3DAnalyzer”. На основе разработанного модуля создана программа для оценки отклонения геометрии изделий от эталонного образца. Представлены результаты тестирования модуля “3DAnalyzer” на примере некоторых поверхностей и основной программы на данных, полученных экспериментально. Описанная здесь технология совмещения точечного множества и поверхности и разработанное программное обеспечение способны обеспечить автоматический контроль геометрии крупногабаритных изделий.

Литература

1.    Самойлов А. А. Применение алгоритма поиска оптимального совмещения дискретного набора точек с 3-D поверхностью для контроля геометрии изделий на предприятии. // XVI Нижегородская сессия молодых учёных. Технические науки: Сборник трудов участников. - Н.Новгород, 2011. ISBN 978-5-93530-345-7, с. 58–62.

2.    Ротков С. И., Попов Е. В., Самойлов А. А. Платонова Н. А. Методика бесконтактного контроля геометрии крупногабаритных изделий. // ПРИВОЛЖСКИЙ НАУЧНЫЙ ЖУРНАЛ, №3(19). Периодическое научное издание. Н.Новгород, ННГАСУ, 2011. 262с. ISSN 1995-2511, №3. с.34-39.