Применение нижних оценок в алгоритмах поиска оптимальных деревьев[1]                                                  

М.В. Губко,
 с.н.с., к.т.н., mgoubko@mail.ru
А.И. Даниленко,
 вед. инж., alexander@danilenko.org
ИПУ РАН, г. Москва

Предлагается схема поиска оптимальных древовидных структур, позволяющая решать задачи построения деревьев решений, оптимизации структуры пользовательских интерфейсов, оптимального кодирования и многие другие. Предлагаемый алгоритм комбинирует методы последовательной индукции, локального поиска и подбора параметров, а также существенно использует нижние оценки затрат иерархии.

 

We suggest an algorithm for optimal tree-shaped hierarchy search. The algorithm can be applied to solve the problems of decision tree growing, user interface structure optimization, optimal coding, and others. The algorithm combines the scheme of sequential top-down tree construction with local search and parameters adjustment. It heavily relies on lower-bound estimates of tree costs.

Введение

Задача поиска оптимальной древовидной иерархии формулируется следующим образом. Каждому направленному дереву H, множество терминальных вершин кото­ро­го является подмножеством заданного множества N, поставлены в соот­ветствие неотрицательные затраты С(H). Необходимо найти дерево с минимальными затратами среди всех деревьев, множество терминальных вершин которых в точности равно N. Множество допустимых иерархий мо­жет быть и более узким, например, состоять только из бинарных деревь­ев. Зада­ча не может решаться перебором, поскольку с ростом числа элемен­тов во множестве N множество над­­стро­ен­ных над N деревьев растет сверхэкспоненциально.

Разработка эффективных методов поиска оп­тимальных иерархий воз­можна для класса, так называемых, секционных функций затрат [1], при ко­торых затраты C(H) иерархии H складываются из затрат с(m, H) ее узлов, а затраты узла m иерархии определяются только разбиением s1, …, sk (k ≥ 2) подчиненной ему группы s Í N (множества элементов N, достижимых из узла m в древовидной иерархии H) между узлами, непосредственно подчиненными узлу m. Таким образом, при секционной функции затраты узла зависят только от того, как устроена иерархия в непосредственной близости от него – сколько узлов подчинено ему непосредственно и какие группы подчинены этим узлам, но не зависят, например, от распределений групп подчиненных узлов. Эти понятия иллюстрируются рисунком 1.

рис.1 К определению секционных функций затрат

За последние годы секционные функции затрат показали свою применимость для описания задач поиска оптимальных иерархий в самых различных предметных областях, включая задачи построения деревьев решений [2], оптимизации структуры пользовательских интерфейсов [3], оптимального кодирования [4], формирования организационной структуры [4, 5], планирования сборочного производства и многие другие.

В докладе описывается схема алгоритма поиска оптимальной древовидной иерархии для произвольной секционной функции затрат. Локальность функции затрат позволяет свести поиск оптимальной структуры к набору частных решений об оптимальном разбиении подчиненной группы текущего узла в ходе последовательного построения дерева сверху вниз. Локальный критерий оптимальности основан на использовании нижних оценок затрат иерархии.

1. Алгоритм поиска оптимальной древовидной иерархии

Предположим, что для любой группы s Í N можно вычислить CL(s) – нижнюю оценку затрат древовидной иерархии, которую можно надстроить над множеством терминальных вершин s (такие оценки были получены для ряда важных подклассов секционных функций затрат, см. [2-6]). В этом случае приближенно оптимальное дерево можно строить «сверху вниз», рекурсив­но. На каждом этапе на основе эмпирического критерия K(s1, …, sk) выбирается число k непосредственно подчиненных узлов и разбиение s1, …, sk между ними группы s, подчи­нен­ной текущему узлу иерархии. В качестве эмпирического критерия удобно использовать взвешенную сумму затрат текущего узла и оценок затрат оптимальных иерархий, которые потенциально можно надстроить над подчиненными ему узлами:

                                     K(s1, …, sk) = c(s1, …, sk) + a(s)×(CL(s1) + … + CL(sk)).                                 (1)

Значение весового коэффициента a(s) определяется в основном сред­ним качеством нижней оценки CL(×). Так, если эта оценка точна, то есть всегда равна затратам оптимальной иерархии, то при a(s) = 1 минимум K(s1, …, sk) по всем допустимым разбиениям s1, …, sk равен затратам оптимальной древовидной иерархии над группой s. Тогда при условии перебора всевозможных допустимых разбиений алгоритм находит точное решение задачи. Чем нижняя оценка CL(×) консер­ва­тивнее, тем, по идее, бóльшим должно быть значение a(s) для того, чтобы сбалансировать в (1) затраты c(s1, …, sk) текущего узла и оценку затрат CL(s1) + … + CL(sk) дочерних иерархий.

Значение коэффициента a(s) в общем случае может зависеть от подчи­нен­ной группы s (чаще – от ее размера |s|) для того, чтобы подстраи­вать­ся под качество нижней оценки для различных групп (в част­нос­ти, под среднее качество оценки для групп разного размера).

Задача полного перебора разбиений может, в зависимости от коли­чес­тва допустимых разбиений, сама быть довольно трудоемкой (полное число разбиений множества из n элементов на непустые подмножества, т.н. число Белла, превышает 50 триллионов уже для n = 20). В этом случае не­об­хо­ди­ма эвристическая процедура неполного перебора разбиений.  В частности, хорошо себя зарекомендовали процедуры локального поиска, например, такие, в которых окрестность разбиения задается с помощью опе­ра­ции объедине­ния пары составляющих разбиение множеств. «Жад­ный» алгоритм выбора разбиения тогда стартует с максимально детального разбиения, на каждом шаге  перебирает «соседние» разбиения и переходит к тому из них, кото­рое доставля­ет минимум эвристическому критерию (1) в том случае, если текущее разбие­ние хуже.

Если окрестность определена с помощью операции объединения множеств, то трудоемкость предлагаемого алгоритма довольно просто  оценить сверху. Пусть вычисле­ние нижней оценки для множества терминальных вершин из n’ элементов требует порядка (n’ – 1)b операций, где b ≥ 1 (оценок более экономных, чем линейные по n’, пока не построено, а оценки со сверхполиномиальной сложностью для подобного алгоритма применять не имеет смысла). Тогда на i-м шаге локального поиска разбиения группы из n’ элементов (заметим, что 1 ≤ i < n’ – 1) имеем текущее разбиение из n’ – i + 1 подгрупп. Следовательно, окрестность разбиения состоит из (n’ – i + 1) (n’ – i) / 2 разбиений, каждое из которых состоит из n’ – i подгрупп. Сумма размеров групп равна n’, причем размер любой подгруппы не менее 1. Для каждой из подгрупп необходимо вычислить нижнюю оценку. Легко показать, что наихудший с точки зрения сложности вычислений случай реализуется, когда имеется одна группа размера i + 1, и n’ – i – 1 групп размера 1. В этом случае для вычисления нижних оценок необходимо порядка ib операций, то есть для выбора наилучшего перехода к соседнему разбиению необходимо порядка ib (n’ – i + 1) (n’ – i) / 2 операций. Суммируя по i от 1 до n’ – 2, получаем общую сложность выбора разбиения порядка n’b + 3 для группы размера n’. Наихудшим для алгоритма является случай т.н. последовательной иерархии [1], в которой разбиение каждой группы состоит из двух подгрупп, одна из которых состоит из единственного элемента. Значит, для вычисления верхней оценки общей сложности алгоритма необходимо просуммировать трудоемкость разбиения групп размера n’ = 2, 3, …, n, что дает порядка nb + 4. Используя эти соображения, можно вычислить и точную формулу верхней оценки сложности. Эта оценка достигается в случае, когда оптимальна последовательная иерархия (в частности, это верно для так называемых сильно сужающих функций затрат [7]), для большинства же возникающих в различных приложениях подклассов секционных функций затрат средняя сложность поиска разбиения существенно ниже.

На практике множество допустимых разбиений зачастую сильно ограничено, что позволяет разрабатывать и другие схемы неполного перебора разбиений, как, например, в рассматриваемой в следующем разделе задаче построения дерева решений.

Еще одна особенность предлагаемого алгоритма состоит в подборе параметра a (а, точнее, в подборе зависимости a(s)) – алгоритм запускается несколько раз при различных зависимостях a(s), и выбирается самое дешевое из построенных деревьев. В последнем разделе доклада описываются методы подбора a(s) и результаты моделирования эффективности работы алгоритма.

2. Пользовательские интерфейсы и деревья решений

Описанная схема алгоритма была опробована при решении двух прикладных задач поиска оптимальных древовидных иерархий – построении дерева решений и оптимизации структуры иерархического пользовательского меню.

Иерархические меню являются популярным методом доступа пользователей к командам и данным. Эффективность меню обычно измеряется средним временем навигации в нем пользователя – чем это время меньше, тем меню лучше. Среднее время навигации существенно зависит от популярности (частоты запроса) отдельных функций информационной системы и от структуры меню: того, в какие категории группируются функции, как эти категории объединяются в метакатегории, и т.д. В результате таких группиро­вок получается древовидная структура, терминальные узлы которой соответ­ству­ют отдельным функциям системы, а остальные узлы – панелям меню или, что эквивалентно, категориям, группам фун­кций. Задача оптимизации структуры меню состоит в том, чтобы среди множества допустимых выбрать структуру, миними­зирующую среднее время пользовательской сессии.

В [6] предлагается алгоритм оптимизации меню, основанный на общей модели навигации в меню [3], нижних оценках времени оптимального меню [4], алгоритмах построения приближенно оптимальных меню, а также учете семантического качества пунктов меню. В данном алгоритме для учета семантических ограничений применяется набор таксономий – классифи­ка­ций функций информационной системы по различным основаниям. Эти таксономии и их комбинации считаются единственными допустимыми способами группировки функций, то есть единственными допустимыми разбиениями (см. предыдущий раздел). Каждому элементу любого допустимого разбиения, таким образом, соответствует некоторое множество функций системы (подчиненная группа терминальных узлов, в терминах предыдущего раздела) и метка – визуальный (или звуковой) образ пункта меню. Каждая группа s Í N (а точнее, соответствующая ей метка) обладает семантическим качеством w(s) – числовой характеристикой, большее значение которой соответствует большему среднему времени доступа к такому пункту меню (типичный пример семантического качества – длина текстовой метки пункта меню).

В задаче оптимизации структуры меню функция затрат узла

                c(s1, …, sk) = m(s1)×с1(k)×s1(w(s1), …, w(sk)) + … + m(sk)×сk(k)×sk(w(s1), …, w(sk)).           (2)

описывает среднее время нахождения пользователя в панели меню из k пунктов, которым соответствуют группы s1, …, sk. Пункты меню имеют семантическое качество w(s1), …, w(sk), и популярности (вероятности быть востребованными пользователем) m(s1), …, m(sk). Функция сi(k) определяет среднее время выбора пользователем i-го пункта меню в панели, состоящей из k пунктов, а неубывающая функция si(w(s1), …, w(sk)) описывает влияние семантического качества всех меток панели меню на время выбора i-го элемента панели.

По сравнению с общей схемой, описанной в предыдущем разделе, предлагаемый алгоритм имеет следующую специфику, связанную с учетом семантического качества и семантических ограничений. Во-первых, так как среднее время нахождения пользователя в панели меню (затраты узла иерархии) зависит от семантического качества пунктов меню, при расчете критерия (1) это семантическое качество непосредственно учитывается. Однако, в то же время, довольно затруднительно построить нижнюю оценку затрат подыерархий, которая учитывала бы семантическое качество пун­ктов меню, составляющих подыерархию. Вместо этого в алгоритме исполь­зуется предложенная в [6] нижняя оценка, в которой предполагается наилучшее семантическое качество пунктов меню, то есть

                                  ,                              (3)

где ms – популярность пункта меню, соответствующего группе s, m(w), w Î s – популярности отдельных функций группы s, и без потери общности считается, что при наилучшем семантическом качестве si(×) = 1.

При этом подстройка под «среднее» семантическое качество производится подбором весового коэффициента a. В описанном в [6] варианте алгоритма коэффициент a принимался равным константе, и пробегал значения от минимального, равного единице, до максимального, соответствующего наихудшему семантическому качеству из всех имеющихся меток. Из иерархий, построенных при различных значениях a, выбиралась структура меню, имеющая минимальное среднее время сессии.

Допустимые разбиения функций в этой задаче ограничиваются заданным набором классификаций по разным признакам. Например, функции офисного приложения логично классифицировать по объекту действия (файл, страница, абзац, перекрестная ссылка, и т.д.), действию (создать, форматировать, удалить и т.д.) и атрибуту объекта (вид, свойства, история и т.д.). Лучше всего использовать иерархические классификации (например, объединяющие такие объекты приложения как перекрестная ссылка и концевая сноска в группу «Ссылки»), поскольку они обладают существенно бóльшими комбинационными возможностями. Тестировались различные эвристики перебора допустимых разбиений – стартующие с максимально детального разбиения и последовательно объединяющие функции в присутствующие в классификации группы, стартующие с наименее детального уровня иерархической классификации и последовательно детализирующие группы функций вниз по уровням классификации, стартующие с «промежуточного» разбиения средней детальности и изменяющие его в сторону как большей, так и меньшей детальности [6].

Реализованный в рамках САПР-системы TheMenuDesigner, этот алгоритм показал приемлемую скорость работы (до одного часа) при оптимизации меню размером вплоть до нескольких тысяч функций и способность строить эффективные структуры меню. Эффективность алгоритма проверялась по близости среднего времени построенных меню и его нижней оценки, рассчитанной исходя из наилучшего семантического качества меток (см. подробнее в [6]).

Деревья решений – хорошо зарекомендовавший себя комплекс методов классификации, распознавания и поддержки принятия решений, применяемых в машинном обучении, идентификации, анализе данных, ситуационном управлении и т.д. Задача обычно состоит в том, чтобы по обучающей выборке построить дерево вопросов, ответы на которые позволяют выбрать то или иное решение. Также важна предсказательная способность дерева – при поступлении на вход новых, ранее не встречавшихся ситуаций (комбинаций ответов) принимать в них правильные решения, то есть те решения, которые принял бы в той же ситуации эксперт.

Дерево решений должно быть компактным – это экономит время при ответах на вопросы; кроме того, эмпирически установлено, что компактные деревья решений обладают лучшей прогностической способностью.

Начиная с 90-х годов прошлого века акцент исследований сдвинулся в сторону построения деревьев решений с учетом различной стоимости вопросов и ошибок классификации. Примеры таких задач – построение вопросников для медицинской диагностики, где стоимость тестов имеет денежную природу, задачи технической диагностики, где стоимости тестов соответствует время принятия решений, задачи ситуационного управления, и многие другие [8].

Давно известно, что задача построения оптимального дерева решений является NP-полной. Более того, известно, что NP-полной является задача аппроксимации оптимального дерева решений с любой наперед заданной точностью. В связи с этим на практике используются многочисленные эвристические алгоритмы, и речь идет скорее об их вычислительной сложности и эффективности на реальных примерах, чем о теоретических оценках. Типичные алгоритмы, как и описанный в предыдущем разделе алгоритм, строят дерево сверху вниз, от корня к листьям, выбирая для каждого узла вопрос на основе легковычислимого эвристического критерия. Отличие же от предложенного выше алгоритма состоит в том, что эвристический критерий обычно представляет собой вариации на тему прироста информации (information gain) [9].

При построении дерева решений элементы обучающей выборки играют роль терминальных узлов, а остальные узлы дерева соответствуют вопросам. Затраты узла соответствуют стоимости вопроса с учетом частоты посещения этого узла и описываются секционной функцией. Действительно, зная допустимый набор групп s1, …, sk легко восстановить вопрос q(s1, …, sk), который делит обучающую выборку на эти группы, и, следовательно, определить стоимость этого вопроса t(q(s1, …, sk)). Затраты узла c(s1, …, sk) = t(q(s1, …, sk))×(m(s1) + … + m(sk)), где m(si) – частота появления ситуаций группы si (можно рассмотреть и более общий случай, когда стоимость вопроса вдобавок зависит от реализовавшейся ситуации – см. объяснения в [2]).

Таким образом, число допустимых разбиений не превышает числа доступных вопросов (обычно, довольно ограниченного), и их можно перебирать полностью, без привлечения локального поиска, аналогично остальным известным алгоритмам построения деревьев решений.

В [2] предложена нижняя оценка стоимости дерева решений, в отличие от известных оценок, имеющая комбинаторную природу. Оценка основана на замене более сложной задачи минимизации средней стоимости определения правильного решения при отсутствии априорного знания о реализовавшейся ситуации более простой задачей минимизации средней стоимости доказательства правильности того или иного решения третьему лицу, не осведомленному о реализовавшейся ситуации. Последняя задача сводится к решению набора комбинаторных задач о минимальном покрытии. Оказывается, что задача о минимальном покрытии, хотя и является NP-трудной, в реальных задачах классификации эффективно решается за время в среднем порядка n×m, где n – объем обучающей выборки, а m – количество имеющихся вопросов. Замена задачи целочисленной оптимизации ее непрерывным аналогом позволяет еще быстрее вычислять нижнюю оценку при минимальных потерях в качестве оценивания.

Предложенную нижнюю оценку можно использовать в формуле (1). В [4] качество работы алгоритма для параметра a, равного единице, сравнивается с качеством работы других известных эвристических алгоритмов, строящих деревья решений. На примере нескольких реальных задач классификации показывается, что предлагаемый алгоритм имеет не худшее качество по сравнению с такими популярными эвристиками как CS-ID3, IDX и EG2.

Недостатком предложенной в [4] нижней оценки является ее относительно высокая вычислительная сложность – порядка n2m. Однако имеется возможность вычислять оценку на основе лишь части обучающей выборки. Полученная огрубленная оценка уже не будет гарантированно нижней оценкой, однако для применения в алгоритме это не обязательно – алгоритм прогоняется несколько раз при различных значениях a (в том числе, и меньших единицы), и в качестве результата его работы выбирается самое дешевое из построенных деревьев.

3. Подбор параметров алгоритма

На качество иерархий, построенных с помощью описываемых алгоритмов, существенное влияние оказывает выбор параметра – зависимости a(s). В настоящем разделе проверяется гипотеза о том, что чем консер­ва­тивнее нижняя оценка, тем бóльшим должно быть значение a(s) для получения наилучших результатов работы алгоритма.

Эта гипотеза обосновывается следующими рассуждениями. Как уже отмечалось, если нижняя оценка всегда совпадает с затратами оптимальной иерархии, то при выборе a(s) = 1 перебор всех допустимых разбиений гарантирует оптимальность иерархии, построенной с помощью описываемых в докладе алгоритмов. В общем случае нижняя оценка CL(N) для множества терминальных вершин N строго меньше затрат оптимальной древовидной иерархии, которые обозначим через Cmin(N). Предположим, что качество нижней оценки (то есть отношение CL(s) / C(s)) одинаково для любых групп s Í N. Тогда, выбрав параметр a(s) равным, например, Cmin(N) / CL(N), мы снова сможем гарантировать построение алгоритмом строго оптимального дерева. В реальности проблема, конечно, в том, что качество нижней оценки не только неизвестно заранее, но существенно (и довольно сложным образом), зависит от s.

Эти соображения, однако, позволяют предложить следующую схему подбора параметра алгоритма a. Запустим алгоритм для a1 = 1 и получим первое приближение – некоторую иерархию H1 с затратами С(H1). Запустим алгоритм снова с параметром a2 = С(H1)/CL(N) и построим иерархию H2. Если она дешевле, чем H1, запустим алгоритм снова с параметром a3 = С(H2)/CL(N), иначе останавливаемся. Алгоритм запускается с уточненным значением параметра до тех пор, пока достигается улучшение результата.

Даже ограничившись двумя итерациями, можно существенно повысить качество алгоритма. Так, сравним алгоритм построения дерева решений с такой популярной эвристикой, как EG2 (также включающей в себя процедуру подбора параметра) на примере стандартного набора данных Cars из набора UCM Machine Learning Repository. Если при a = 1 рассматриваемый алгоритм давал результаты не хуже, чем EG2 в 28% случаев для случайных стоимостей вопросов из диапазона [0, 1], то при добавлении второй итерации – уже в 57% случаев (73% против 40% в случае, когда стоимости вопросов зависят от реализовавшейся ситуации).

В то же время, далеко не всегда именно при a = С(H) / CL(N) достигаются наилучшие результаты работы алгоритма. Так, на рисунке 2 показаны две типичные зависимости затрат результирующей иерархии от a (а точнее, от нормированного параметра ; k = 1 соответствует a = С(H)/CL(N)) в задаче оптимизации пользовательского меню (имеется 792 функции и четыре иерархических таксономии). В одном случае наилучшая иерархия получается при k = 0,6, в другом – при k = 1,4. Как видно из рисунка, может иметься несколько локальных минимумов, поэтому если позволяют вычислительные мощности, для получения наилучших результатов стоит запускать алгоритм для диапазона значений k, например, от нуля до двух, и выбирать самую дешевую из построенных иерархий.

 

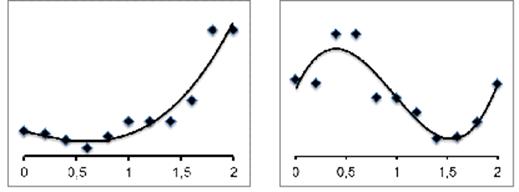
рис. 2 Зависимость затрат иерархии от нормированного параметра k

Качество нижней оценки CL(N) обычно зависит от размерности задачи |N|, поэтому определенный выигрыш можно получить, варьируя зависимость a(|s|). Имея иерархию, построенную на первом шаге алгоритма при a = 1, можно для группы s, подчиненной каждому из ее узлов, вычислить a(s) как отношение затрат подыерархии с корнем в этом узле, и нижней оценки CL(s), а затем подобрать зависимость a(|s|) методом наименьших квадратов. В то же время, в рассматриваемых приложениях относительный выигрыш от варьирования зависимости a(|s|) несущественен.

Заключение

В докладе рассмотрена универсальная схема алгоритма поиска оптимальной иерархии для секционной функции затрат. Применение схемы иллюстрируется на примерах построения дерева решений и оптимизации пользовательских меню. Для применения схемы алгоритма к некоторой прикладной задаче необходимо построить нижнюю оценку затрат оптимальной иерархии, наподобие тех, что были рассмотрены выше. Перспективы исследований связаны с построением эффективных алгоритмов поиска приближенно оптимальных иерархий для других приложений, в которых имеются нижние оценки затрат иерархии, например, в описанной в [4] модели надстройки иерархии управления над сетью технологических взаимодействий исполнителей. Эта задача относится к области организационного дизайна. Исходными данными является граф потоков материалов, финансов и информации между рядовыми сотрудниками организации или между отдельными производственными операциями бизнес-процессов компании. Эти потоки должны контролироваться, для чего над исполнителями (операциями) надстраивается иерархия управления. Подчинение группы исполнителей менеджеру предполагает делегирование ему прав контроля потоков между исполнителями этой группы. Содержание каждого менеджера сопряжено с затратами, зависящими от объема контролируемых им технологических потоков, и описываемыми секционной функцией. Задача состоит в надстройке над заданным графом технологических взаимодействий древовидной иерархии, имеющей минимальные затраты.

Для этой модели имеется простая нижняя оценка затрат иерархии, однако построение алгоритма требует разработки экономных схем перебора разбиений для довольно крупных множеств исполнителей (состоящих из нескольких тысяч элементов).

Литература

1.   Воронин А.А., Мишин С.П. Оптимальные иерархические структуры. М.: ИПУ РАН, 2003.

2.   Goubko M.V. Lower-bound Estimate for Cost-sensitive Decision Trees // Preprints of the 18th IFAC World Congress, Milano (Italy), August 28 - September 2, 2011. P. 9005-9010.

3.   Goubko M. V., Danilenko A. I. An automated routine for menu structure optimization // Proceedings of the 2nd ACM SIGCHI symposium on Engineering interactive computing systems, Berlin, Germany, June 19-23, 2010. p. 67-76.

4.   Губко М.В. Математические модели оптимизации иерархических структур. М.: ЛЕНАНД, 2006.

5.   Губко М.В., Мишин С.П. Оптимальная структура системы управления технологическими связями / Материалы международной научной конференции «Современные сложные системы управления». Старый Оскол: СТИ, 2002. С. 50–54.

6.   Губко М. В., Даниленко А. И. Оптимизация иерархических структур с учетом индивидуальных характеристик узлов иерархии // Труды VIII Всероссийской школы-семинара молодых ученых "Управление большими системами", 25-28 мая 2011 года, Магнитогорск: Изд-во ГОУ ВПО "МГТУ", 2011. C. 313-316.

7.   Мишин С.П. Оптимальные иерархии управления в экономических системах. М.: ПМСОФТ, 2004.

8.   Turney, P. Types of cost in inductive concept learning. Workshop on Cost-Sensitive Learning at ICML, 2000. P. 15–21.

9.   Quinlan, J.R. Discovering rules by induction from large collections of examples. In D. Michie (Eds.) Expert systems in the microelectronic age, Edinburgh University Press, Edinburgh. 1979. P. 168–201.

 


[1] Работа выполнена при финансовой поддержке Российского фонда фун­да­мен­таль­ных исследований (проект 10-07-00129).