Интеграция управления при синтезе сложных систем в условиях нечёткого регулирования
А.С. Степанова,
аспир. каф. КРЭМС, ser23n2005@yandex.ru,
Д.Ю. Муромцев,
д.т.н., проф., зав. каф. КРЭМС, crems@crems.jesby.tstu.ru,
ТТТУ,
г. Тамбов
Проведён
анализ интеллектуальных систем в условиях мягких вычислений. Показана
необходимость кластеризации нечёткой логики в мягких вычислениях гибридных
систем. Учитывая триаду критериев: эффективность-стоимость-время, показана
необходимость использования интеграционного метода управления, построенного по
двухуровневому принципу, основанному на втором законе К. Гёделя. Предложен
интеллектуальный концепт информационно – управляющей сложной человеко-машинной
системы, использующей нечёткое регулирование, для обеспечения быстрого принятия
решения в критических ситуациях, сохраняющих жизнь человека.
The analysis of intelligent systems in terms of soft computing. Brought the need for
clustering of fuzzy logic in soft computing. Given the triad of criteria:
cost-effectiveness-time shows the need for integrative management approach
built on a two-level principle, based on the second law of K. Godel. We propose
the concept of intelligent information - managing a complex man-machine system
using fuzzy control, to ensure quick decision-making in critical situations,
preserving human life.
Введение. В последнее время в отечественной и
зарубежной литературе наиболее существенное внимание уделяется методам и
способам построения сложных систем, к которым относится, например, вооружение и
военная техника (ВВТ) [1,3,5]. Сложная система вызывает объективную
необходимость увеличения количества решаемых задач, скорости ее обработки,
увеличения объема обрабатываемой информации.
Клод Шеннон предложил научную модель информатизации физических
процессов, рис.1.
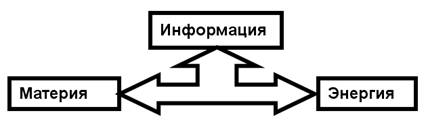
рис. 1 Модель
информатизации физических процессов
Современна электроника — основная технология, которая позволяет
нам контролировать не только материа-льное, но и энергетическое и
информационное взаимодействие. В промышленных процессах информация сейчас
действует с помощью интеллектуального управления. Интеллектуальные системы
управления, в свою очередь, используют методы искусственного интеллекта.
Математическая теория
нечетких множеств (fuzzy sets) и нечеткая логика (fuzzy logic) продолжают
привлекать внимание исследователей в области интеллектуальных, экспертных
систем, а также систем поддержки принятия решений. Эти понятия были впервые
предложены американским ученым Лотфи Заде (Lotfi Zadeh) [9,10]. Основной
причиной появления новой теории стало наличие нечетких и приближенных
рассуждений при описании человеком процессов, систем, объектов. Управление
сложным объектом в реальных условиях связано не только со сложностью
математического, программного, информационного и технического обеспечения, но и
недостаточностью информации, необходимой для управления и принятия управленческих
решений.
Проблема. В последнее десятилетие отмечается
гибридизация методов интеллектуальной обработки информации. Мягкие вычисления
объединяют такие области, как нечеткая логика, искусственные нейронные сети,
извлечение знаний, базы данных, вероятностные рассуждения, эволюционные
алгоритмы и другие. Они дополняют друг друга и используются в различных
комбинациях для создания гибридных интеллектуальных систем.
Традиционно при
конструировании сложных систем в условиях неопределенности используют
вероятностные подходы, в соответствии с которыми неопределенность описывается
критериями, характеризующими возможность проявления наперед заданных
результатов [1,4,6]. Для получения удовлетворительных характеристик систем
управления в последнее время появился целый ряд методов, основанных на
структурной и параметрической адаптации управляющих устройств [9].
Искусственный интеллект (ИИ) уже используется в более
развитых средствах промышленного контроля и управления, дополняющих классические
технологии управления, направленные на создание новых изделий, систем с более
дешёвыми и короткими производственными циклами.
Технологии ИИ
включают в себя искусственные нейронные сети (ИНС), экспертные системы (ЭС),
нечеткую (fuzzy) логику (НЛ), генетические алгоритмы (ГА). Лежащие в их основе
идеи существенно отличаются от общепринятых методов вычислений, имитируя
человеческие, то есть более понятные технологу, чем программисту.
Мягкие вычисления. Мы рассмотрим
системы с кластеризацией нечеткой логики, которые оперируют такими дефинициями, как
неопределенность и частичная/приблизительная истина. Данные методы
предназначены для решения очень сложных нелинейных задач, которые либо
превышают возможности общепринятых алгоритмических методов, либо требуют для
своего решения слишком больших материальных и временных затрат.
Нечёткая логика (НЛ)
добилась успехов в программных средствах, в контроллерах и в интегральных схемах.
Контроллеры на базе нечеткой логики выпускают Fuji Electric, Klockner-Moeller,
Rockwell-Automation/ Allen-Bradley, Siemens и Yokogawa и другие. Дополнительные
возможности для нечеткой логики дает объединение производителей контроллеров с
поставщиками программных средств.
Главной задачей по мере расширения прикладных областей
становится превращение НЛ в средство проект-ирования для различных аппаратных и
программных платформ. В некоторых случаях НЛ-технология уже использу-ется в
расширении по программированию на базе нечеткой логики (Fuzzy Logic
Programming). Оно использовано для стандарта IEC 1131 (программируемые
контроллеры). Структура МЭК 1131-7 представлена на рис. 2.
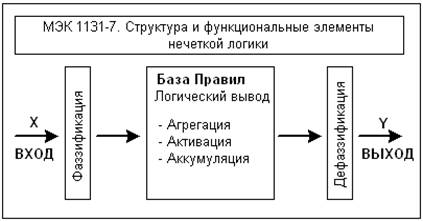
рис. 2 Стандарт IEC
1131-7. Программирование на базе нечёткой логики. Определяет НЛ – компоненты и взаимодействие НЛ - модулей с другими языками
программирования
В качестве выходных
данных могут выступать измеряемые технологические параметры, расчётные величины
и контрольные значения. Выходными данными являются реальные параметры в форме
корректирующих величин.
IЕС/МЭК 1131-7 уже
лежит в основе НЛ-структуры и программного пользовательского интерфейса пакета
fuzzyTech компании Inform, который внедряется в известный пакет ISaGRAF (CJ
International). Объектно-ориентированный пакет fuzzyTech интегрирует функции
нечеткой логики со стандартным ПЛК (А-В, Modicon и Siemens) и с популярными программными
средствами управления процессами типа Citech (Ci Technologies) и InTouch
(Wonderware). Версия fuzzyTech (5.0) оптимизирована для использования под
управлением Windows. Скорость вычислений на базе нечеткой логики может
сравняться со скоростью вычислений традиционными методами, позволяя свести
управляющие циклы до долей миллисекунды.
Технологии ИИ находят
все большее применение в таких областях, как управление движением и двигателями.
Для решения задач ближайшего будущего разработчики могут использовать
классические методы регулирования, однако через пару лет любой инженер будет
значительно больше разбираться в том, как использовать это мощное средство для
решения таких задач, как MES (исполнительная производственная система), ERP
(управление предприятием), MRP (планирование материальных ресурсов) диагностику
и прогнозирование.
Можно
сказать, что комбинация методов ИИ может повысить мощь и устранить недостатки систем регулиро-вания.
Каждая технология ИИ имеет свои особенности. Сочетание методов даст великолепные
результаты.
Чтобы использовать объединённые
методы, необходимо радикально изменить образ мышления.
Постановка задачи. Как известно, возможность точного
математического описания сложной системы отсутствует [1,4]. Классический подход
к синтезу сложной системы, предполагающей иерархическое построение, состоит в
разбиении большой системы на более мелкие компоненты: уровни, подсистемы, блоки
и т.д., к которым далее применяются известные методы проектирования [1].
Поэтому сложную систему, как это обычно делают при проектировании вооружения и
военной техники, разбивают на подсистемы, каждую из которых представляют соотношением
[2,6]:
![]() , (1)
, (1)
где X={x1,…,
xn} – множество элементов xi системы, а R обозначает
закономерности поведения системы, включающие правила действия с элементами xi,
взаимосвязи между различными xi, соотношения между Х и внешней
средой, ограничения и управления.
Для реализации
сложной системы необходимо также знать выходную величину системы – выходной
вектор YТ=(y1, …, ym), алгоритм нахождения которого обычно
составляется в терминах {вход-выход}. При заданных множествах X, R, этот алгоритм
представляет отображение:
![]() ,
(2)
,
(2)
где ui –
управляющее воздействие в подсистеме. Наиболее типовая ситуация управления,
когда R известно лишь приближенно. Тогда результаты наблюдения за X и Y могут
быть использованы для коррекции алгоритма управления, в части множества R.
В практике построения
систем управления сложными объектами получила широкое распространение триада
критериев: эффективность-стоимость-время.
Кроме того, следует отметить, что в вооружении и военной технике более
предпочтительным является задача, когда главным критерием используется
стоимость, а два других выступают в качестве ограничений [2,9].
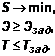 (3)
(3)
Существующие подходы
к синтезу систем в условиях неполной информации опираются на методы нечеткой
логики, методы адаптации, методы обучения.
Методы нечеткой логики. В системах с нечеткой логикой по
информации, выраженной в лингвистической форме, ставится задача формирования
управляющего воздействия на объект управления. Текущая информация yα,
yi (рис. 3) о функционировании системы с помощью процедуры фаззификации
преобразуется в лингвистические величины вида отрицательная и положительная,
большая, средняя, малая для формирования лингвистической переменной, например,
ошибки управления. В нечетком вычислительном устройстве (контроллере) с помощью
базы правил ЕСЛИ-ТО осуществляется формирование логического решения. На
основании полученного логического решения процедурой дефаззификации получается
единственное численное значение управляющего воздействия U на выходе
контроллера. Структура системы управления при управлении по принципу нечеткого
вывода показана на рис. 3.
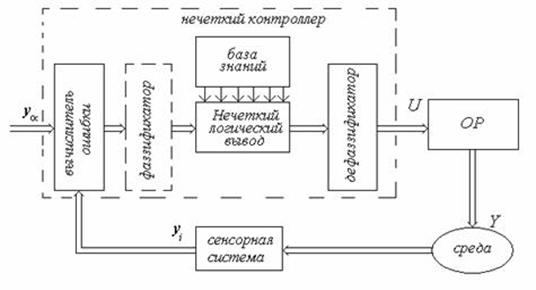
рис. 3 Структура
системы с нечеткой логикой управления
Сложность построения
системы с нечеткой логикой заключается в эвристичности алгоритмов фаззификации
и дефаззификации. Эту сложность возможно избежать, если в распоряжении
конструктора имеется достаточно адекватная функция принадлежности или модель
системы. В этом случае настройка системы управления значительно упрощается, в
противном случае она оказывается сложной. Различные варианты алгоритмов
фаззификации и дефаззификации представлены в [2]. Дополнительную трудность
работе контроллера создают помехи и внешние возмущения, кроме того вопросы компенсаций
возмущений не изучены ещё до конца [2,6].
Методы адаптации. Структура типовой адаптивной системы
стабилизации объекта в условиях неизмеряемых возмущений ξt c
использованием для целей управления точечных оценок ct показана на
рис. 4.
Адаптивная система
управления построена по иерархическому принципу, в соответствии с которым
система управления имеет два уровня. На верхнем уровне расположено устройство,
реализующее непосредственно алгоритм адаптивного управления А (адаптер),
изменяющее вектор настроечных параметров ct управляющего устройства
УУ, расположенного на нижнем уровне.
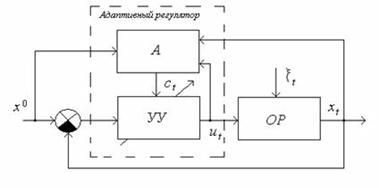
рис. 4 Структура
адаптивной системы управления
Управляющее
устройство реализовано по принципу обратной связи, формирует управляющие
воздействия ut так, чтобы компенсировать текущие ошибки системы.
Алгоритм нижнего уровня выражен в виде операторного уравнения:
![]() , (4)
, (4)
где θ=x0-xt
– значение текущей ошибки системы. Уравнение (4) называют алгоритмом (законом)
управления. Алгоритм верхнего уровня, который в символьной форме может быть
представлен так:
![]() ,
(5)
,
(5)
называют алгоритмом (законом) адаптации. Для
реализации закона адаптивного управления требуется информация о задающем
воздействии, текущем значении управляющего воздействия, формируемого на
основании предыдущих значений вектора параметров, и реакция объекта на эти воздействия.
Уравнения (4), (5)
определяют алгоритм адаптивного управления. Объект совместно с управляющим
устройством образуют основной контур регулятора, а цепь обратной связи,
включающая адаптер, образует контур адаптации. Для формирования управления ut
и определения вектора подстраиваемых параметров ct, исходя из
практики обычно используют конечную часть предыстории процесса настройки
параметров.
Как показывают авторы
[8] существует эффект переключения контроллеров: системы коммутации, который может
быть потенциально дестабилизирован соответствующим выбором переключения, даже
если это переключения между системой с числом Гурвица стабильно замкнутого цикла. Это переключение из одного режима в
другой может привести к катастрофе. Мгновенные переключения двумя разными
контроллерами могут приводить к неконтролируемым переходным режимам и
нестабильности. Этот эффект не может быть объяснен обычной теорией систем с
точки зрения частотного анализа, поскольку его основная передаточная функция,
определяется для нулевых начальных условий, в то время как реальное приложение,
как правило, ненулевое. Изучая системы, нужно рассматривать нулевые начальные
условия и не упрощать математические модели, так как в этом проявляется
конкретное поведение системы. Это помогает сравнивать системы между собой,
обеспечивая строительство общей теории систем. Но с другой стороны, это переключение может
произвести к неожиданным сбоям в конкретных условиях.
Мгновенные переключения двумя разными контроллерами могут
приводить к неконтролируемым переходным режимам и нестабильности. Этот эффект
не может быть объяснен обычной теорией систем с точки зрения частотного анализа,
поскольку его основная передаточная функция определяется для нулевых начальных
условий, в то время как реальное приложение, как правило, ненулевое. Например,
в редких и непредсказуемых ситуаций, возмущениях, при переключении между
автопилотированием и переходом на ручное пилотирование возможно ввергнуть
самолет в роковую аварию. Надежных отчетов о таких несчастных случаев не так
легко найти, но это признаётся единодушно [2,8].
Методы обучения. Современные методы обучения опираются на
алгоритмы обучения распознаванию образов, при этом систему управления
конструируют по принципу организации нейронной сети, которая в техническом
исполнении представляет сетевой компьютер (или нейрокомпьютер). Работы,
проводимые в США, Финляндии и других странах по использованию сетевых компьютеров
для управления «Облачными вычислениями» (Cloud Computing), подчеркивают актуальность такой организации
системы управления. Cloud Computing предполагает перенос
вычислительных ресурсов в Интернет.
В процессе обучения
ИНС присутствуют наибольшие ошибки системы управления. Кроме того, может
оказаться так, что большие значения весовых коэффициентов могут сместить
рабочую точку регулировочной характеристики в область насыщения, при малых
изменениях весов сеть перестает обучаться.
При применении
алгоритмов градиентного спуска в качестве настройки возможно попадание в
область локального, а не глобального минимума функции ошибки обучения. Чтобы
алгоритм сходился, приращения весов, а, следовательно, и скорость обучения
должны быть малы, но тогда сеть будет обучаться долго по времени. Чрезмерно
большая скорость обучения приводит к неустойчивости процесса. Таким образом,
задача настройки сети представляет определенную сложность для конструктора.
Сравнительная характеристика. В отличие от
классической теории управления, где закон управления, выражает некую
математическую зависимость управляющей переменной от входной, в нечетком
регуляторе закон управления представляется набором правил логического выбора
вида ЕСЛИ-ТО в зависимости от значений лингвистической переменной, принадлежность
которой к некоторому лингвистическому терму (множеству) устанавливается так
называемой функцией принадлежности. Функционально необходимыми элементами
нечетких регуляторов являются: база правил, блок формирования логического
решения, блоки фазификации и дефазификации. Строгих рекомендаций по выбору
алгоритмов фазификации и дефазификации нет и следствием этого является грубость
получаемой системы управления. Таким образом, самостоятельное использование
нечеткого регулятора приводит к построению системы управления с низким качеством
управления.
Исходными данными для
всех случаев построения являются фазовые координаты системы (например, ошибка и
ее производные). В качестве выходной информации при нечетком выводе информации
и сетевом подходе к реализации системы управления используется один и тот
сигнал – управляющее воздействие на объект управления. Результатом
функционирования адаптивной системы является параметры системы управления,
которые могут быть использованы только сетевой системой управления. Недостатком
адаптивных систем является наличие затрат времени на адаптацию системы, которое
в свою очередь является платой за незнание параметров системы. Для получения
высокого качества в системе ошибочное функционирование системы на период
настройки системы управления должно быть каким-либо образом скомпенсировано.
Значит, самостоятельное использование адаптивной системы, как и сети нежелательно
с точки зрения временных характеристик системы. Целесообразно их совместное
использование, где адаптивная система управления выполняет своеобразный
механизм настройки сети.
Таким образом, для
повышения эффективности функционирования системы управления сложным объектом
целесообразно объединить методы, основанные на принципах нечеткого вывода
информации и сетевом принципе, использующем адаптивные методы настройки сети.
Этому способствует наличие одинаковой входной и выходной информации при обоих
подходах.
Интеграция методов. Предлагается
система управления сложным объектом, построенная по двухуровневому принципу,
основанном на втором законе К. Гёделя о неполноте, при котором нижнему уровню
отводится непосредственное формирование управление объектом (рис. 5). На нижнем
уровне находятся нечеткий
контроллер
НчК и контроллер сети (НК). Используется новая технология «Облачных вычислений»
[7].
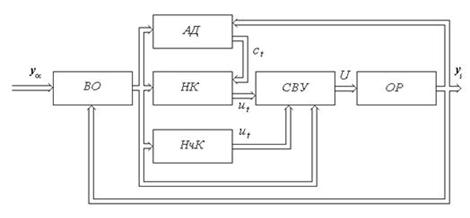
рис. 5 Структура
интегральной системы управления
Окончательный выбор
управления системой объект (ОР) выполняется системой выбора управления СВУ,
осуществляющей выбор управления по величине сигнала ошибки, поступающего с
вычислителя ошибки ВО. Предполагается, что в виду грубости системы, то есть
когда ошибки находятся в диапазон I, рис. 6, то в системе управление
выполняется НчК. При достижении ошибок диапазона II система выбора управления
СВУ переключает на управление от вычислительного устройства на сетевой принцип,
осуществляющий периодическую корректировку по математической модели процесса.
Предполагается, что времени для переключения настройки в этом случае достаточно
и не может привести к неожиданным сбоям в реальных условиях.
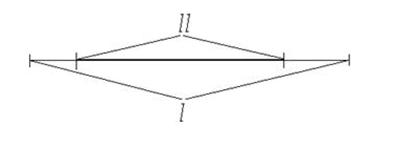
рис.6 Диапазоны
работы систем управления
Полагаем, что
структура системы управления, представленная на рис. 5, будет иметь лучшие
показатели эффективности продолжительности и точности отработки заданий, за
счет комплексного использования методов. Ее реализация приведет к сокращению
материальных затрат на разработку каждого отдельного устройства с требуемыми
показателями эффективности и, кроме того, позволит получить прирост
эффективности функционирования системы в целом, за счёт уменьшения цикла
управления реальным объектом.
Выводы. Рассмотренные методы проектирования сложных
систем являются основным инструментом современных разработчиков, занимающихся
конструированием сложных технических систем в условиях априорной неопределенности.
Эффективность их применения определяется базой знаний, опытом проектирования и навыками
разработчиков. Наибольшего эффекта следует ожидать в комплексном интеграционном
подходе в проектировании системы.
Возможность построения самоорганизующихся структур, при рациональном
использовании рассмотренных методов, позволит рассчитывать на получение синергетического
системного эффекта: уменьшении времени разработки (быстрого выхода на первичный
рынок) и обеспечения необходимого управления в реальных условиях.
Литература
1.
Воронин
А.Н. Сложные технические и эргатические системы: методы исследования / А.Н.
Воронин, Ю.К. Зиатдинов, А.В. Харченко. – Харьков: Факт, 1997. – 240 с.
2.
Митрахович
М.М. Интеграция методов при синтезе сложных систем в условиях априорной неопределённости.
3.
ААЭКС,
2008. №2(22). Режим доступа свободный: http://aaecs.org/mitrahovich-mm-integraciya-metodov-pri-sinteze-slojnih-sistem-v-usloviyah-apriornoi-neopredelennosti.html.
4.
Михалевич
В.С. Об одном подходе к исследованию процесса управления уровнями вооружений /
В.С. Михалевич, В.М. Кунцевич. – Киев. 1989. – 26 с. (Препр. / АН УССР. Ин-т
кибернетики им. В.М. Глушкова).
5.
Растригин Л.А. Адаптация сложных систем / Л.А. Растригин. – Рига:
Зинатне, 1981. – 375 с.
6.
Трапезников
В.А. Управление и научно-технический прогресс / В. А. Трапезников. – М.: Издательство
ИПУ РАН, 1985/2005. – 223 с.
7.
Цвиркун А.Д. Основы синтеза структуры сложных систем / А.Д.
Цвиркун. – М.: Наука, 1982. – 200 с.
8. By SARAH J. WACHTER Beaming to the Cloud All the Mess That Is Our Digital
Life Published: The New York Times, October 24, 2010.
http://www.nytimes.com/2010/10/25/technology/25iht-clutter25.html?src=busln.
9. Dan Simon. Truth,American Culture, and Fuzzy Logic.
http://academic.csuohio.edu/simond/pubs/317101.pdf.
10. L. A. Zadeh, Toward a Logic of Perceptions Based on Fuzzy Logic, in: V.
Novak, I. Perfilieva (Eds.), Discovering the World With Fuzzy Logic.
Springer-Verlag, Heidelberg (Studies in Fuzziness and Soft Computing, Vol. 57),2000,
pp. 4-28.
11. Zade L. A. The concept of a linguistic variable and
its application to approximate reasoning. Part 1, 2, 3 // Information Sciences,
n. 8 pp.199-249, pp.301-357; n. 9 pp. 43-80.