Сравнение алгоритма двумерных матриц и муравьиного алгоритма для задачи геометрического покрытия

В.Д. Фроловский,
зав. каф., д.т.н., проф., frolovsky@asu.cs.nstu.ru,
НГТУ, г.Новосибирск,

С.Л. Забелин,
аспир., zabelinsl@mail.ru,
СибГУТИ, г. Новосибирск

Муравьиный алгоритм — один из эффективных полиномиальных алгоритмов для решения задач максимального геометрического покрытия. Его эффективность подтверждается программной реализацией в данной работе

ACO algorithm designed for the network routing problem, is described in detail

Введение

Области применения задач максимального геометрического покрытия охватывают большое количество сфер деятельности человека. Они появляются в системах воздушного и космического наблюдения, системах безопасности, агротехнических системах, системах проектирования и др.

Актуальность данной задачи обусловлена также её принадлежностью к классу NP-трудных задач, сложность которых очень быстро возрастает с увеличением размерности. Для решения задач малой размерности можно использовать точные алгоритмы. Однако для задач большей размерности точные методы требуют значительных временных затрат и не дают хороших результатов. Эффективным является использование метаэвристических методов.

1. Методы геометрического покрытия

1.1. Метод двумерных матриц

Пусть в двумерном пространстве имеется покрываемая поверхность и покрывающие геометрические объекты (ГО) _,где – общее количество заданных объектов различной формы (прямоугольники, треугольники, окружности и их теоретико-множественные комбинации). Требуется расположить ГО на покрываемой поверхности таким образом, чтобы вся поверхность была покрыта целиком.

В двумерной матрице M каждая ячейка представляет собой точку на плоскости (Ox; Oy), описанной множеством точек T. Ячейки могут содержать только три различных значения (0,1,2).: 0 – точка лежит за пределами области, либо уже данная точка была покрыта, 1 – точка лежит внутри области, не была покрыта, 2 – точка является границей области.

В алгоритме покрытия двумерными матрицами реализован принцип покрытия прямоугольной области предметами по следующему правилу: самый большой подходящий предмет входящий в область, то есть не переходящий за границы области (цифра 2) в матрице M, заменяет цифры 1 и 2, которые находятся между самой верхней левой точкой Lv и точкой , и если на нули. Количество использованных предметов увеличивается на 1 (параметр ). Если данный предмет не удовлетворяет условие , то берется следующий предмет, меньший по площади. Таким образом, алгоритм покрывает всю поверхность области, до тех пор, пока последняя цифра в матрице M не будет «покрыта» нулем. То есть пока отношение общей площади S прямоугольной области к сумме всех площадей предметов, которые были использованы в покрытии данной поверхности, не будет равно единице:

(1)

Данный алгоритм сокращает избытки материала и покрывает всю поверхность.

1.2. Муравьиный алгоритм

Муравьиный алгоритм (алгоритм оптимизации подражанием муравьиной колонии, англ. ant colony optimization, ACO) — один из эффективных полиномиальных алгоритмов для нахождения приближённых решений задачи коммивояжёра. Подход предложен бельгийским исследователем Марко Дориго (Marco Dorigo).

В основе алгоритма лежит поведение муравьиной колонии — маркировка более удачных путей большим количеством феромона. [2]. Работа начинается с размещения муравьёв в вершинах графа (городах), затем начинается движение муравьёв — направление определяется вероятностным методом.

Решение не является точным и даже может быть одним из худших, однако, в силу вероятности решения, повторение алгоритма может выдавать (достаточно) точный результат.

Идея муравьиного алгоритма – моделирование поведения муравьёв, связанного с их способностью быстро находить кратчайший путь между двумя точками и адаптироваться к изменяющимся условиям, находя новый кратчайший путь. При своём движении муравей метит путь феромоном, и эта информация используется другими муравьями для выбора пути. Это элементарное правило поведения и определяет способность муравьёв находить новый путь, если старый оказывается недоступным.

Предлагается использовать следующую модификацию муравьиного алгоритма для решения задачи максимального геометрического покрытия.

Вначале муравей располагает набором из всех геометрических объектов и покрываемой поверхности . Объекты последовательно размещаются на поверхности. Муравей выберет объект для размещения на очередной пустой области поверхности в соответствии с распределением:

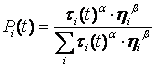(2)

Эвристическая информация задается величиной , которая равна площади объекта, и значением феромона .

, (3)

где – интенсивность испарения;

– значение критериальной функции для наилучшего решения, найденного с момента начала поиска. Таким образом, чем лучше решение (чем меньше ), тем больше феромона оставляет муравей.

В процессе работы алгоритма, геометрические объекты с большей вероятностью попадают на те места, на которых они в среднем дают лучшие результаты (и оставляют больше феромона).

2. Реализация алгоритма покрытия двумерными матрицами

В алгоритме реализован принцип покрытия области предметами по следующему правилу: самый большой подходящий предмет, входящий в область, т.е. не выходящий за границы области и не пересекающий других объектов, заменяет -1 своим индексом (индексом из очереди объектов), в занимаемых им ячейках в матрице S0. Если данный предмет не подходит, т.е. он выходит за границы области или пересекает другой (уже уложенный объект), то берется следующий предмет, меньший по площади. Таким образом, укладка объектов продолжается до тех пор, пока последний предмет не будет уложен.

3. Реализация муравьиного алгоритма

Начало цикла.

Для всех объектов считаются вероятности по формуле (1).

Эвристическая информация задается величиной , которая равна площади объекта, и значением феромона .

Объекты сортируются по убыванию вероятности и по порядку размещаются на области, с тем условием, что при укладке объект по возможности не выходит за края области, подсчитывается количество пересечений (точек растра, где фигуры накладываются друг на друга) для каждого объекта.

Обновляется значение феромона для каждого объекта (2).

- вычисляется по формуле

где - площадь i-того объекта (количество точек растра, из которых состоит объект)

- количество пересечений i-того объекта с другими (точек растра, где фигуры накладываются друг на друга).

Выход из цикла поиска: если не было ни одного пересечения объектов, и выхода за границы области, если достигнуто требуемое количество итераций.

4. Работа с программой

Работа с программой делится на 2 этапа: ввод данных; выбор алгоритма и просмотр результата.

Ввод данных организован с помощью графического редактора, на котором представлена: панель рисования объекта (левая клавиша мыши рисует «клетку» объекта, правая клавиша мыши стирает «клетку» объекта), панель списка объектов (нулевой объект – область на которую размещают остальные объекты) и панель управления списком объектов.

Проведён ряд экспериментов, которые показали, что муравьиный алгоритм работает эффективней алгоритма двумерных матриц.

Литература

1. Бабаев, Ф. В. Оптимальный раскрой материалов с помощью ЭВМ / Ф. В. Бабаев. – М: Машиностроение, 1982. – 168с.

2. Bilchev, G. Evolutionary metaphors for the bin packing problem / G. Bilchev // Proceedings of the Fifth Annual Conference on Evolutionary Programming, Cambridge, MA. – 1996. – P.333–341.