Управление профилактическим обслуживанием технических

систем по эмпирической функции надежности

В.П. Полетаев,

Д.А. Богданов
Вологодский государственный технический университет,
danger@mh.vstu.edu.ru, г. Вологда

Любая техническая система проходит ряд этапов жизненного цикла, на которых решаются различные аспекты надежности. На первых этапах разработки и конструирования системы формируются основные показатели качества разрабатываемой технической системы - безотказности и ремонтопригодности, разрабатывается система встроенного автоматизированного контроля состояний системы в целом и отдельных ее частей. На последующих этапах - испытаний различного вида эти показатели проверяются. И, наконец, на заключительном этапе — этапе эксплуатации эти показатели проявляются.

Таким образом, идея разработки и создания системы реализуется на заключительном этапе - этапе эксплуатации.

Каждая система создается для эксплуатации и получения определенного эффекта от ее работы. Отсюда следует особая роль этапа эксплуатации, поскольку все усилия, затраченные на создание высококачественной системы, могут быть сведены на нет неправильно или нерационально организованной эксплуатацией.

С другой стороны, эксплуатация технических систем с низкими характеристиками надежности также может привести к значительным потерям и существенно снизить эффективность их использования.

Важнейшей проблемой на этапе эксплуатации является определение такой периодичности технического обслуживания, которая позволит минимизировать суммарные потери, учитывающие затраты времени и средств на обслуживание и потери в результате ухудшения качества функционирования объекта.

В работе [1] показано, что оптимальное значение периодичности обслуживания можно найти как решение уравнения

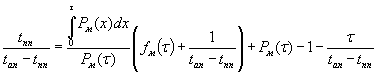(1),

а можно с помощью формулы

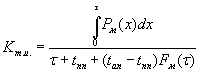(2)

по положению максимума , рассчитав его зависимость от . В формулах использованы следующие обозначения: - периодичность обслуживания; - функция распределения времени работы без скрытых отказов; - вероятность работы без скрытых отказов (функция надежности); - среднее время, затраченное на проверку состояния объекта; - средняя длительность планово-аварийного обслуживания, включающего проверку состояния и последующее восстановление работоспособности.

При использовании любого из способов нахождения значения решение будет зависеть от выбора вида , т.е. функции распределения времени работы без скрытых отказов, которая определяет и вид функции надежности .

Ниже приведены результаты исследования уравнения (1) для различных законов распределения времени безотказной работы. В качестве исходных материалов использованы статистические данные о надежности приборов контроля линейных размеров, полученные при их реальной эксплуатации в условиях автоматизированного подшипникового производства. Исходя из характера построенных гистограмм времени безотказной работы, установлено, что такой вид функции плотности распределения могут иметь несколько известных распределений – гамма распределение, распределение Рэлея, распределение Вейбулла, нормальное распределение.

При решении вопроса о том, какой из теоретических законов распределения наилучшим образом согласуется с эмпирическим распределением, для каждого теоретического закона в соответствии с критерием Пирсона была рассчитана величина

,

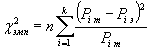где - число объектов наблюдения, равное для нашего случая 60; , - соответственно теоретическая и экспериментальная вероятность попадания случайной величины в i-ый интервал.

В приведенной ниже табл.1 указаны значения и значения вероятности того, что в силу чисто случайных причин мера расхождения между теоретическими и эмпирическими распределениями будет меньше, чем . Под объектом 1 и объектом 2 подразумеваются различные типы объектов наблюдения.

Таблица 1

Сравнение опытных и теоретических распределений

Вид распределения	Объект 1		Объект 2
Гамма-распределение	1,426	0,984	4,370	0,735
Распределение Рэлея	3,691	0,882	6,033	0,644
Распределение Вейбулла	2,855	0,897	5,618	0,587
Нормальное распределение	6,703	0,465	11,256	0,134

Как видно из табл.1 сравнение опытных и теоретических распределений приводит к неоднозначному результату, т.к. все указанные распределения можно принять для описания наблюдаемых на практике распределений, поскольку во всех случаях вероятность выше минимально допустимого уровня, равного 0,1. Хотя гамма-распределение наилучшим образом описывает статистические данные, при расчете оптимальной периодичности технического обслуживания в исследовательских целях рассматривались все четыре вида распределения.

Решение уравнения (1) для поиска оптимального осложняется двумя обстоятельствами. Первое из них – это невозможность получить в явном виде выражении для , поэтому для различных при заданных значениях и проводился расчет правой части уравнения (1) - функции . По таблице значений находилась величина , при которой левая часть уравнения (1) равна правой.

Второе обстоятельство заключается в том, что используемая в уравнении функция надежности имеет аналитический вид только для распределений Рэлея и распределения Вейбулла, интегральная же функция 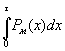не имеет аналитического вида для всех типов распределений. В связи с этим при выполнении расчетов с использованием программы Mathcad для каждого вида распределения указывался конкретный вид функции плотности распределения вероятностей , а функция надежности определялась как .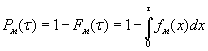

В табл.2 приведены результаты расчетов по уравнению (1) для объекта 2 при различных соотношениях параметров и .

Таблица 2

Значения оптимальной периодичности обслуживания

Вид распределения, параметры	, час	/=2	/=5	/=10
		, час
Гамма-распределение с параметрами 0,001074269 1/час, =2,369837871.	1	690	688	683
	5	821	809	791
	10	889	867	836
Распределение Рэлея с параметром =1974 час.	1	226	225	222
	5	385	377	366
	10	482	468	447
Распределение Вейбулла с параметрами =1,576, =2206 час.	1	144	142	141
	5	266	261	252
	10	346	336	320
Нормальное распределение с параметрами =2206час, =1433 час.	1	145	156	172
	5	302	323	352
	10	410	434	468

Аналогичные расчеты для других объектов показывают, что существенно зависит не только от вида, но от параметров закона распределения. В соответствии с табл.2 очевидна также зависимость оптимальной периодичности обслуживания от времени, потраченного на оценку состояния объекта и времени восстановления работоспособности в случае скрытого отказа.

Помимо уравнения (1) для нахождения использовалось и выражение (2). Вначале вычислялись значения с большим шагом изменения , чтобы установить диапазон, в котором находится максимум. Затем в этом диапазоне вычисления велись с мелким шагом, для определения , при котором коэффициент технического использования достигает максимума. Как и следовало ожидать, результаты в обоих случаях совпадают, что свидетельствует о точности предложенной для расчета математической модели.

Предложенная математическая модель является универсальной и позволяет оптимизировать периодичность проведения обслуживания технических систем. При этом главным вопросом объективности принятия решения о величине становится проблема адекватной оценки статистической информации с целью определения вида закона распределения времени безотказной работы.

В реальных ситуациях, пример которой описан выше, часто достаточно сложно отдать предпочтение тому или иному закону распределения времени безотказной работы, не опасаясь совершить субъективную ошибку. Очевидно, что наиболее точный результат может быть получен только на основе первичной статистической информации о надежности, характеризующей поведение функции надежности и входящей как в уравнение (2), так и в уравнение (1) по которым вычислялось оптимальное значение периодичности обслуживания .

Было исследовано поведение функции надежности для тех типов распределения, которые указаны в табл.2 для всего диапазона оптимальных значений . Представленные на рис.1 графики показывают, что зависимость функции надежности от времени достаточно уверенно можно рассматривать как линейную, описываемую формулой

, (3)

где - коэффициент, характеризующий поведение функции .

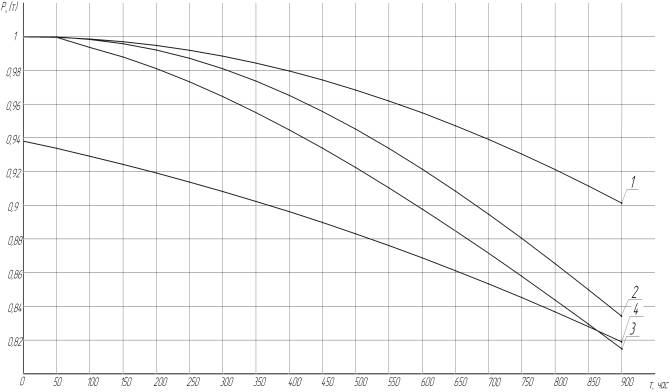
рис. 1 Эмпирические графики функции надежности:

1-распределение Рэлея;

2-гамма-распределение;

3-распределение Вейбулла;

4-нормальное распределение.

Для получения наиболее точных результатов в диапазоне изменения может быть выполнена кусочная аппроксимация зависимости уравнением (3). При этом значения коэффициента на различных участках могут быть найдены, например, методом наименьших квадратов.

Используя выражение (3) и подставляя его в формулу (2), получаем для

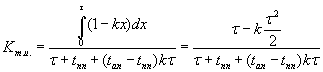. (4)

Для нахождения оптимальной длительности периодичности обслуживания по критерию максимума найдем производную

.

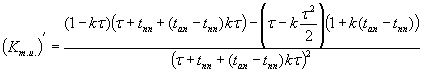Приравняем числитель 0 и раскроем скобки:

.

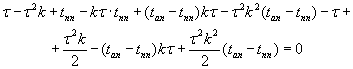После приведения подобных величин получим уравнение:

.

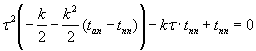Разделим обе части полученного уравнения на :

.

Решая квадратное уравнение

,

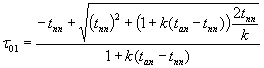после несложных преобразований окончательно имеем

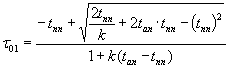. (5)

Таким образом, предложена аппроксимирующая математическая модель оптимизации периодичности обслуживания технических систем, необходимого для обеспечения их эффективной эксплуатации.

Литература

1. Управление периодичностью обслуживания технических систем при оптимизации коэффициента технического использования / В.П. Полетаев, Д.А. Богданов // Труды международного симпозиума «Надежность и качество», ПГУ, том № 1, 2007. – С. 237 – 239.