Изоморфизм и толерантный изоморфизм

П.А. Правильщиков
С.н.с., к.т.н.
ИПУ РАН, г. Москва

По мере развития науки человечество всё больше и больше освобождается от собственных мифов, в том числе и от научных мифов. Так, ещё в античные времена Архимед, восхищённый созданной им теорией рычага первого и второго рода воскликнул: «Дайте мне точку опоры, и я переверну Землю!». Переворот Земли с помощью рычага с точки зрения современного инженера – это миф. Тогда же, в античные времена Птолемей утверждал, что Земля является центром Вселенной. Солнце, планеты и все остальные звёзды обращаются вокруг неё. Такая научная концепция является древним вариантом антропного принципа, который позднее был назван антропоцентризмом. Эта концепция, этот миф продержался более 1500 лет до коперниканской научной революции. Заметим, что главными двигателями этой революции были Галилей и Кеплер. Первый изобрёл телескоп, второй ¾ на основе данных Т. Браге показал, что Земля и другие планеты двигаются вокруг Солнца не по круговым, а по эллиптическим орбитам. Им же были установлены законы обращения планет вокруг Солнца (законы Кеплера). Коперник же, как не рядовой иерарх католической церкви, осторожно говорил о своей гелиоцентрической системе мира, как о гипотезе.

Позднее, в XVIII веке достигла своего расцвета философско-методоло-гическая доктрина, известная под названием «детерминизм» или «механистический детерминизм». В своей крайней форме эта доктрина была выражена французским математиком и физиком П. С. Лапласом. Поэтому эту доктрину часто называют «лапласовским детерминизмом». Своё понимание детерминизма Лаплас рассматривал как методологический принцип построения всякой науки. Ограниченность лапласовского детерминизма проявилась в попытке объяснить весь мир, в том числе физиологические, психические и социальные явления, с точки зрения механистического принципа детерминизма. Образец окончательной формы научного познания Лаплас видел в небесной механике. И это не смотря на то, что именно он является, по сути, создателем математической теории вероятностей, в которую ввёл так называемые производящие функции. До него первые шаги в этой области были сделаны Б. Паскалем, П. Ферма, Я. Бернулли. Лаплас же привёл их выводы в систему, усовершенствовал методы доказательств, сделав их более строгими и менее громоздкими. Позднее он доказал теорему, носящую его имя, развил теорию ошибок и способ наименьших квадратов, позволяющие находить наивероятнейшие значения измеренных величин и степень достоверности этих подсчётов. Классический труд Лапласа «Аналитическая теория вероятностей» издавался много раз. Только при его жизни он издавался трижды — в 1812, 1814 и 1820. В качестве введения была помещена его работа «Опыт философии теории вероятностей» (1814), в которой разъяснялись основные положения и значение теории вероятностей.

Но не смотря на столь важные результаты в теории вероятностей, Лаплас твёрдо придерживался принципа детерминизма и утверждал, что ес-ли ему дадут данные о начальном состоянии тел во Вселенной, то можно вычислить её состояние в любой момент времени. Это утверждение он от-носил, как к частному случаю, и к Солнечной системе. В XX веке мы узнали, что это был очередной научный миф, так как на практике не всегда легко предсказать, какой будет система в конце своего существования, да-же если известны начальные условия. Например, довольно просто рассчитать орбиту единственной планеты, обращающейся вокруг Солнца (это, так называемая, задача двух тел была решена ещё Ньютоном). Но, введите еще одну планету в систему, и все значительно усложнится, так как в результате будет получена известная в небесной механике задача трёх тел, которая, как было показано, не имеет точного решения. Например, если рассмотреть движение Земли вокруг Солнца с учётом третьей планеты (например, Юпитера), то такая задача точного аналитического решения не имеет. Здесь сила гравитационного притяжения, действующая между планетами, определяется по формуле Ньютона:

	,	(1)
где g ¾ универсальная гравитационная постоянная, одна и та же для всей Вселенной, g = 6,67 ´10^-11 м3 × кг ^-1 × с ^-2; m1 и m2 ¾ массы первого и второго тела соответственно, а r ¾ расстояние между телами.

Если в соответствии с (1) вычислить величину силы F_☼Å, действующей между Солнцем и Землёй (т.е. между m_☼ и m_Å), а затем вычислить по той же формуле величину силы F_J притяжения Земли Юпитером (масса которого превосходит массу остальных восьми планет, вместе взятых), то окажется, что F_J / F_☼ < 0,0006. Отсюда следует, что сила F_J взаимного притяжения планет в задаче трёх тел ничтожно мала по сравнению с силой F_☼ притяжения Земли Солнцем. Ещё меньшими являются силы притяжения других планет, действующие на Землю. Но эти силы существуют! И их наличие может привести к заметному эффекту на больших промежутках времени. Под их действием траектория Земли будет постепенно отклоняться от траектории, по которой в настоящее время Земля движется вокруг Солнца. Если рассмотреть изменение за один год современной траектории T_Å Земли, т. е. превращение её в другую траекторию T_Å,1, то траектория T_Å,1 будет мало отличаться от исходной траектории T_Å. Новая траектория T_Å,1 будет сходной траекторией с траекторий T_Å. Однако, и это следует подчеркнуть, траектория T_Å и траектория T_Å,1 не будут одинаковыми: T_Å ¹ T_Å,1.
Точность, с которой в наше время астрономы могут предсказывать солнечные затмения и движение планет, наводит на мысль, как когда-то она убедила Лапласа, что динамика тел в Солнечной системе абсолютно предсказуема. На самом деле это впечатление обманчиво. Регулярным движение планет кажется лишь в тысячелетнем масштабе. Но, когда счет идет на миллионы лет, в их динамику вполне может вмешаться хаос. В XX веке ученые пришли к пониманию того, что в природе имеются системы, полностью детерминистические в ньютоновском смысле, тем не менее, их будущее состояние с точки зрения практического применения не поддается расчетам даже с применением самых современных суперкомпьютеров. Это явление, известное как детерминистический хаос, стало предметом изучения теории хаоса, которая в наши дни является областью активных научных исследований. Суть теории хаоса состоит в том, что в некоторых естественных системах небольшие изменения начальных условий приводят к огромным изменениям на выходе.

Большинство известных нам систем в природе не такого типа. В них небольшие изменения на входе приводят к небольшим изменениям на выходе. Однако теперь мы знаем о существовании и таких систем, которые гораздо чувствительнее к начальным условиям и в которых различие в восьмом знаке после запятой оказывает значительное влияние на конечный результат. Хаотическая система определяется как система, в которой выход экспоненциально зависит от изменений на входе. В XX веке мы узнали, что в природе существуют системы, в которых исход конкретной ситуации существенно зависит от измерения воздействия на входе и будущее поведение которых непредсказуемо для всех практических применений.
Дело в том, что когда мы (или тот же П.С. Лаплас) говорим об «определении» начального состояния, мы фактически говорим об измерении. Каждое измерение в реальном мире содержит погрешность. Например, если измерить длину стола линейкой, на которой наименьшее деление — миллиметр, то в измерении неизбежно будет присутствовать ошибка в долю миллиметра. Таким образом, для хаотических систем теоретически возможно предсказать будущий исход, но только в тех случаях, когда начальное состояние можно определить с абсолютной точностью. Поскольку такой точности достичь невозможно, эти системы для всех практических применений непредсказуемы. При этом важно понимать, что существование детерминистического хаоса не нарушает принципа детерминизма. Так, в XX веке мы узнали, что система может быть детерминистической и предсказуемой теоретически, в то же время, оставаясь непредсказуемой на практике. Этот вывод выглядит как насмешка над амбициями Лапласа.
Но, возвращаясь к сходным траекториям T_Å и T_Å,1, заметим, что относительно недавно были проделаны вычислительные эксперименты, где были заданы начальные положения и скорости планет, чтобы запустить моделирование их движения в течение какого-то промежутка времени. Параллельно с этим было запущено второе моделирование, в котором было всё то же самое, только начальные данные в положении планет и их траектории отличались на незначительную величину, например, всего на 1 миллиметр. Вначале моделирования орбиты планет в этих двух ситуациях с огромной точностью совпадали, но постепенно, с ходом времени, они начали всё сильнее и сильнее различаться. Для регулярного (нехаотического) движения это различие оставалось небольшим, в то время как для хаотического движения — экспоненциально увеличивалось со време-нем. Вычисления такого рода для разных планет Солнечной системы не так давно были проделаны несколькими группами учёных. Они, в част-ности, доказали, что движение планеты Плутон становится хаотичным на временах порядка 10-20 миллионов лет из-за специфического резонансного взаимодействия с  другими планетами. Динамика внутренней Солнечной системы, которая включает первые четыре планеты от Солнца – Мер-курий, Венеру, Землю и Марс, — тоже хаотична на масштабе 4-5  милли-онов лет, правда в  этом случае причина хаоса пока не известна. Важно отметить следующее. И в случае использования математического аппарата классической механики, и в случае использования аппарата теории хаоса происходит постепенное изменение траекторий. От начальной траектории T_Å идёт переход к некоторой сходной траектории T_Å,1, затем к траектории T_Å,2, сходной с траекторией T_Å1. Затем происходит переход к сходным траекториям T_Å,3, T_Å,4 и т.д. К этому сходству траекторий, вычисленных с помощью аппаратов различных теорий, мы ещё вернёмся.
В настоящее время некоторые специалисты не исключают, что наличие регулярных движений планет Солнечной системы и в то же время наличие хаотических движений, которые ныне связывают с резонансными явлениями, приведёт к тому, что реальная динамика Солнечной системы поставит перед теорией динамических систем уже вопросы не прикладного, а фундаментального характера. В такой ситуации понадобится и новый математический аппарат, отличный как от аппарата классической механики, так и от формализмов теории хаоса. Возможно, таким аппаратом окажется аппарат теории толерантности и подобия, так как в XX веке абсолютная точность, абсолютное равенство и абсолютная одинаковость стали подвергаться сомнению. В XXI веке эта «сомнительная» тенденция продолжается.
Вместо жёсткой формальной логики с её абсолютными «да» и «нет» в XX веке появилась нечёткая логика. И теперь традиционную формальную логику можно рассматривать как её частный случай. Вместо теории множеств со строгим определением элемента множества появилась теория нечётких множеств. В этой теории определить, что элемент m_i принадлежит множеству M можно лишь с некоторой вероятностью. Как продолжение этой тенденции в XX веке на смену логическим уравнениям пришли нечёткие уравнения, и теперь мы всё больше и больше осознаем, что в природе не существует абсолютной точности, абсолютного равенства, как не существует и абсолютной одинаковости, которые можно рассматривать в качестве очередного научного мифа. Более того, почти одновременно с нечёткой логикой и нечёткой теорией множеств в XX веке появился математический аппарат, позволяющий выразить не одинаковость объектов, а их сходство. На смену одинаковости, математической экспликацией которой является бинарное отношение эквивалентности, пришло понятие сходства, математической экспликацией которого является отношение толерантности. Отношение эквивалентности является всего лишь частным случаем отношения толерантности.
В данной работе предлагается осуществить дальнейшее развитие теории толерантности и подобия [2]. Это развитие заключается в переходе от одного из основных понятий современной математики: идеально строгого изоморфизма к более реалистическому понятию называемому толерантным изоморфизмом. Традиционное классическое понятие изоморфизма, по мнению автора, является абсолютизацией, и, следовательно, очередным научным мифом. Эта абсолютизация изоморфизма, пригодная для идеальных объектов, во многом аналогична абсолютизации понятия одинаковость. Повторим, что экспликацией понятия одинаковость является бинарное отношение эквивалентности. Поэтому совсем не случайным является то, что отношение изоморфизма считается отношением эквивалентности.
Определение 1. Изоморфизм ¾ взаимнооднозначное соответствие (отображение) между  алгебраическими системами, сохраняющее отношения и операции.
Понятие изоморфизма полезнее и проще всего в целях данной работы проиллюстрировать на двух графах G_i(V,E) и G_j(W,I), у которых одинаковое число вершин и одинаковое число дуг (ребер). Два графа G_i(V, E) и G_j(W, I) называются изоморфными, если существует взаимно-однозначное соответствие между множествами вершин V, W и множествами рёбер E, I, сохраняющее отношение инцидентности. Толерантный изоморфизм отличается от традиционного изоморфизма, например, тем, что свойства не-которой одной вершины v_in графа G_i заметно отличаются от свойств соответствующей вершины v_jm графа G_j. Такие графы часто встречаются в фи-зике, в химии, в теории программирования, в теории САПР и технической диагностики, а также в работах, связанных с CALS-технологиях — см. [1, 2]. Теперь, чтобы ввести такое понятие, как толерантный изоморфизм, нам понадобится привести определение отношения эквивалентности и определение отношения толерантности.
Определение 2. Отношение E на множестве M называется эквивалентностью (или отношением эквивалентности), если существует разбиение {M₁, M₂, …} множества M такое, что соотношение xEy выполняется тогда и только тогда, когда x и y принадлежат некоторому общему классу M_i данного разбиения.
Напомним, что систему непустых подмножеств {M₁, M₂, . . .} множества M называют разбиением этого множества, если
1) M = M₁ È M₂ È . . . и 2) M_i Ç M_j = Æ при i ¹ j.
Понятие эквивалентности является математической экспликацией обыденного понятия одинаковости. Переход от расплывчатого понятия “одинаковость” к точно определённому типу отношений сопровождался введением нового математического термина “эквивалентность”. Бинарное отношение эквивалентности обладает свойствами транзитивности, симметричности и рефлексивности. Так, в геометрии подобие треугольников может служить примером отношения эквивалентности. Если, например, DABC ~ DDEF, а DDEF ~ DKGH, то DABC ~ DKGH. Этот пример характеризует свойство транзитивности отношения эквивалентности и, в частности, отношения подобия треугольников. Понятно также и свойство симметричности подобия: что если DABC ~ DDEF, то и DDEF ~ DABC. И, конечно же, DABC ~ DABC ¾ свойство рефлексивности (DABC всегда подобен самому себе). Одинаковость объектов, выражаемая отношением эквивалентности, означает их полную взаимозаменяемость в некоторой ситуации.
Так же, как переход от расплывчатого понятия “одинаковость”, к точно определённому типу отношений сопровождался введением нового математического термина “эквивалентность”, математическое отношение, соответствующее нашему интуитивному представлению о сходстве или неразличимости, получило в математике название “толерантность”. Заметим, что одинаковость – это идеализация неразличимости. Выше уже отмечалось, что в действительности не существует абсолютно одинаковых объектов. Существуют объекты, которые мы не можем различить, так как все наши измерения проводятся с некоторой степенью точности. Если с помощью измерений не удаётся различить два объекта, то такие объекты мы привыкли считать одинаковыми. На самом деле они не являются таковыми: они просто неразличимы. Часто с появлением новых поколений приборов, удаётся различить объекты, ранее считавшиеся одинаковыми (примером могут служить многие астрономические объекты: звёзды, галактики и квазары). Более того, считается, что в принципе в макромире (в быту и в традиционной механике) можно измерить координату и импульс с произвольной точностью. Однако в квантовой механике один из основных её законов – принцип неопределённости – запрещает одновременное из-мерение координаты и импульса с произвольной точностью, поэтому различимость квантовых объектов достаточно ограничена. Отсюда некоторые квантовые объекты пока считаются «одинаковыми».
Неразличимость является превосходной степенью сходства, а вовсе не одинаковости, как может показаться на первый взгляд. Одинаковость ¾ свойство качественно иное. Дело в том, что неразличимые объекты (так же, как и сходные) не разбиваются, вообще говоря, на классы так, чтобы в каждом классе элементы не различались, а элементы разных классов заведомо различались. Разумеется, одинаковость есть частный случай неразличимости и сходства, так же, как эквивалентность (математическая экспликация одинаковости) есть частный случай толерантности (математической экспликации сходства). Чтобы более глубоко пояснить этот момент приведём определение толерантности.
Определение 3. Отношение T на множестве M называется толерантностью (или отношением толерантности), если оно рефлексивно и симметрично.
Другими словами, для всякого m_i Î M существует ,по крайней мере один, m_j Î M, такой, что m_iTm_j :

" mi $ mj½mi, mj Î M Þ miTmj.

(2)

Естественность приведённого выше определения 3 и выражения (2) видна из того, что всякий объект заведомо неразличим сам с собой и, уж подавно, похож на себя: m_iTm_i (это и выражает рефлексивность отношения толерантности: "m_iÎM [m_iTm_i]). Ясно также, что два объекта сходны или не сходны независимо от порядка, в котором они рассматриваются. Это обстоятельство выражается симметричностью отношения толерантности: "m_i, m_j ÎM [m_iTm_j Þ m_jTm_i]. Но вот транзитивность для сходства (толерантности) совсем не обязательна:

"mi,mj, mk ÎM [ miTmj & mjTmk ØÞ miTmk].

(3)

Поясним это на множестве M толерантных слов: M ={w₁,w₂,w₃} = {срок, сток, стог}. Пару слов (w_i,w_j) из множества M будем называть толерантными, если слова этой пары отличаются при написании не более, чем в одной букве. Например, пара слов (w₁,w₂) = (срок, сток) различаются только в одной букве. Так как предполагается, что на множестве M задано отношение толерантности, то для каждого слова в M существует толерантное ему слово. Другая пара (w₂,w₃) = (сток, стог) слов из M так же является па-рой толерантных слов. Но пара слов (w₁,w₃)=(срок, стог) уже не является парой толерантных слов, так как отличаются они уже в двух буквах. Этот пример иллюстрирует то, что бинарное отношение толерантности не обладает свойством транзитивности (3). И именно поэтому эквивалентность является частным случаем толерантности.

Если одинаковость объектов означает их полную взаимозаменяемость в некоторой ситуации, то сходство ― это частичная взаимозаменяемость. Частичная взаимозаменяемость означает возможность замены ¾ замены с некоторыми (допустимыми в данной ситуации) потерями и с допустимым риском. Если для объектов указано только сходство, то их невозможно разбить на чёткие классы. Чёткое разбиение означает такое разбиение, когда внутри класса объекты похожи, а между объектами разных классов сходства нет. В случае сходства возникает размытая ситуация без чётких границ. Каждый элемент множества несёт определённую информацию о похожих на него элементах. Но не всю информацию, как в случае одинаковых элементов. Здесь уже нет дилеммы: “Всё или ничего” или “Полная информация — отсутствие информации”. Здесь возможны разные уровни информации, которую один элемент содержит относительно другого. Так, в физике и в химии часто используется понятия «совершенный» и «ограниченный» (или «несовершенный) изоморфизм. Физическое понятие «совершенный» изоморфизм соответствует традиционному изоморфизму в математике. «Ограниченный» (или «несовершенный) изоморфизм в математике, насколько известно автору, до сих пор не рассматривался.
Однако и в физике, и в химии существует достаточно много объектов, соответствие которых можно выразить понятием «несовершенный изоморфизм». Впервые это было показано немецким минералогом Э. Мичерлихом в 1819 г. на примере молекул KH₂PO₄, KH₂AsO₄ и (NH₄)H₂PO₄ (читатель может сравнить толерантные формулы с толерантными словами, приведёнными выше, рассматривая обозначения химических элементов как буквы). Вскоре было обнаружено, что первые два вещества образуют смешанные кристаллы («твёрдые растворы») с единой внешней формой при произвольном отношении фосфора и мышьяка (P : As), в то время как в других парах аналогичные замещения ограничены количественно. Отсюда важным отличием кристаллов от слов, в которых буквы расположены последовательно, является пространственное расположение атомов в кристаллической решётке. Другим отличием является то, что атомы, в
отличие от букв, обладают определёнными свойствами, например, свойствами, определяющими их валентность. Поэтому для кристаллов, как и для графов, имеющих сходное строение, имеет смысл говорить об изоморфизме, но не о традиционно идеальном математическом изоморфизме и не об ограниченном, недостаточно строгом физическом изоморфизме, а о толерантном изоморфизме.

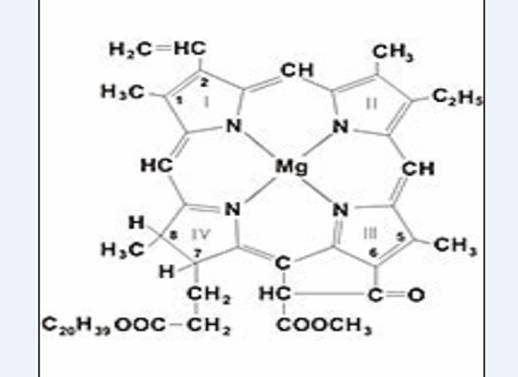
Рис. 1. Структурная формула хлорофилла.

Кроме кристаллов другим примером толерантного изоморфизма может служить сходство структур молекул хлорофилла (рис. 1), состоящего из 136 атомов (С₅₅H₇₀N₄O₆Mg), и двух гемов (основной части гемоглобина крови всех животных). Первый входит в состав крови человека, придавая ей красный цвет. Его химическая формула — С₅₅H₇₀N₄O₆Fe. Второй гем встречается в голубой крови некоторых морских животных (например, осьминогов). Его формула — С₅₅H₇₀N₄O₆Cu. Отсюда можно видеть, что сложная структура многоатомной молекулы хлорофилла отличается от структуры «красного» гемоглобина только одним атомом магния: вместо атома магния, входящего в состав молекулы хлорофилла, в молекуле «красного» гемоглобина расположен атом железа. Молекула «голубого» гемоглобина в крови осьминога отличается от молекулы «красного» гемоглобина тоже в одном атоме. Так, вместо атома железа, входящего в состав молекулы «красного» гемоглобина, в состав молекулы «голубого» гемоглобина входит атом меди (см. выше).

В данной работе сделана попытка устранить некоторый пробел в математике и ввести строгое понятие толерантного изоморфизма для такого не слишком строгого физического понятия как «ограниченный» (или «несовершенный») изоморфизм. Здесь же хотелось бы также изложить основные свойства этого понятия и обосновать его практическую полезность. Практическая полезность толерантного изоморфизма неразрывно связана с толерантным выводом (или толерантной трансляцией), которая позволяет осуществлять вывод нового объекта, структура которого толерантно изоморфна оригиналу. Толерантный вывод основан на определённых принципах, которые уместно напомнить: принцип соответствия, принцип законосообразности и принцип иерархии толерантности (принцип иерархии сходства) — см. [1, 2]. Важную роль в толерантном выводе играет также принцип сохранения (непрерывности) предиката. Принцип сохранения предиката утверждает, что любые операции (предикаты) определённые на расширенной области, для элементов исходного (расширяемого) класса должны иметь те же значения, что и определённые на исходной области одноимённые операции (предикаты). Традиционным примером, на котором иллюстрируется этот принцип, является доопределение арифметических операций (например, сложения), определённых первоначально для натуральных чисел, на область целых (в том числе и отрицательных) чисел. Более детально указанные принципы изложены в [1,2].

Теперь прежде чем, привести примеры толерантных алгоритмов, важно заметить, что иногда разработчики новых алгоритмов не знают, что разрабатываемый ими «новый» алгоритм для автоматизации некоторых функций или операций в той или иной области знания или инженерной практики, по сути, не является новым, а имеет сходный ему, т.е. толерантный прототип. Это ещё объясняется и тем, что два или более толерантных алгоритма могут быть записаны на различных алгоритмических языках (например, два алгоритма могут быть записаны на двух языках: на языке С⁺⁺ и на языке Паскаль или Турбо Паскаль). Следует подчеркнуть, что для выявления толерантности двух алгоритмов следует записать их на одном языке, например, на специально разработанном для этого языке T-тран [1]. Заметить также, что в теории сложности часто используется сводимость одних алгоритмов к другим. Особенно часто приём сводимости одного переборного алгоритма к другому применяется к алгоритмам, предназначенным для решения так называемых труднорешаемых (NP-полных) задач. Так, недавно сотрудник нашего института А.В. Марковский показал, что алгоритм решения нечётких уравнений сводится к алгоритму решения одной из NP-полных задач — задаче поиска минимального покрытия. Не трудно видеть, что сводимость алгоритма решения одной задачи к алгоритму решения другой задачи возможна только тогда, когда между двумя алгоритмами существует определённая общность. Другими словам, когда оба алгоритма являются сходными алгоритмами.

Теперь следует привести примеры толерантных алгоритмов, начиная с простейших. В качестве простейшего алгоритма для вычисления силы F гравитационного взаимодействия двух тел можно рассмотреть тот же закон Ньютона (1). В качестве толерантного ему рассмотрим известный закон Кулона для электростатических взаимодействий тел. Закон Кулона для определения силы F, действующей между двумя электрически заряженными телами, имеет вид:

	,	(4)
где e - диэлектрическая постоянная, определяющая свойства среды (для вакуума диэлектрическая проницаемость или электрическая постоянная e0 = 8,854 187 817… ×10^−12 Ф·м^−1 ); e1 и e2 ¾ величина заряда первого и второго тела соответственно, а r ¾ расстояние между телами.

Законы (1) и (4) получили название законов обратных квадратов, так как сила F находится в обратной зависимости от квадрата расстояния между телами. Алгебраическая форма их записи обладает несомненным сходством. Последнее становится особенно заметным, если учесть, что электрон был открыт более, чем на 100 лет, позднее (в 1897 г.), чем закон Кулона (1785 г.). Во времена Кулона под электричеством понимали некую положительную и отрицательную электрическую жидкость, обладающую специфической массой. Электрический заряд рассматривался как некоторая величина массы этой электрической жидкости, заполнявшей тело. Тогда закон Кулон был записан по аналогии с законом Ньютона (1):

	,	(5)
где e ¾ та же диэлектрическая постоянная, определяющая свойства среды; m1 и m2 ¾ величина заряда первого и второго тела соответственно (т.е. масса электрической жидкости, заполняющей первое и второе тело), а r ¾ расстояние между телами.

Теперь можно пойти ещё дальше и записать выражения (1) и (5) в виде последовательности алгебраических символов, обозначающих постоянные, переменные и символы операций:

F = g×m1×m2 / r^2
	(6)
F = e×m1×m2 / r^2

Закон Ньютона и закон Кулона, представленные в форме (6) можно рассматривать как последовательности символов или тексты алгоритмов для вычисления значения силы F. Эти алгоритмы записаны на некотором (алгебраическом) языке. Не трудно видеть, что запись двух законов в фор-ме (6) аналогична записи толерантных слов, приведённых выше. Тексты этих простейших алгоритмов, представляющих собой линейные последовательности, являются толерантными в том смысле, в каком являются толерантными приведённые выше слова: они отличаются не более чем в одном символе. Как известно, толерантность записи законов в (6) отражает не только внешнее, формальное сходство, но и некоторые внутренние содержательные аспекты такого сходства. В современной физике согласно стандартной модели взаимодействий элементарных частиц всякое взаимодействие между телами осуществляется путём обмена теми или иными частицами. В случае закона Ньютона такими частицами являются пока ещё не обнаруженные опытным путём гравитоны. В случае закона Кулона такими частицами являются фотоны (в частности, виртуальные фотоны). Частицы, излучённые одним телом, пересекают шаровую поверхность с радиусом r. С ростом радиуса r число частиц, пересекающих единицу шаровой поверхности, уменьшается в обратной зависимости от r². Следовательно, в такой же зависимости ослабевает гравитационное и электростатическое взаимодействие двух тел, что и отображают законы (1) и (4). Конечно же, выражения в (6) можно рассматривать как вырожденный простейший случай вычислительных алгоритмов. Известная в теории алгоритмов теорема Бёма и Джакопини утверждает, что всякий алгоритм, всякая программа могут быть построены из трёх различных структурных элементов: линейной последовательности операторов, альтернативы if … then …. else и итерации (цикла). Поэтому здесь следует привести в качестве примера толерантные алгоритмы, содержащие линейные последовательности, альтернативы (ветвления) и циклы. В качестве таких алгоритмов будут приведены алгоритмы построения тестов для трёх различных классов объектов диагностирования: дискретных (цифровых) устройств, программ и аналоговых устройств.

Для аналоговых устройств многие алгоритмы были, как утверждают их авторы, созданы независимо от алгоритмов построения тестов для дискретных устройств, хотя впоследствии они оказались сходными с соответствующими алгоритмами для цифровых устройств. Для программ алгоритмы построения тестов были созданы автором уже на основе существующих алгоритмов построения тестов для дискретных устройств, некоторые из которых были разработаны им самим [3]. В [3] алгоритмы построения тестов для программ уже рассматривались как распространение известных алгоритмов на новый класс объектов диагностирования.
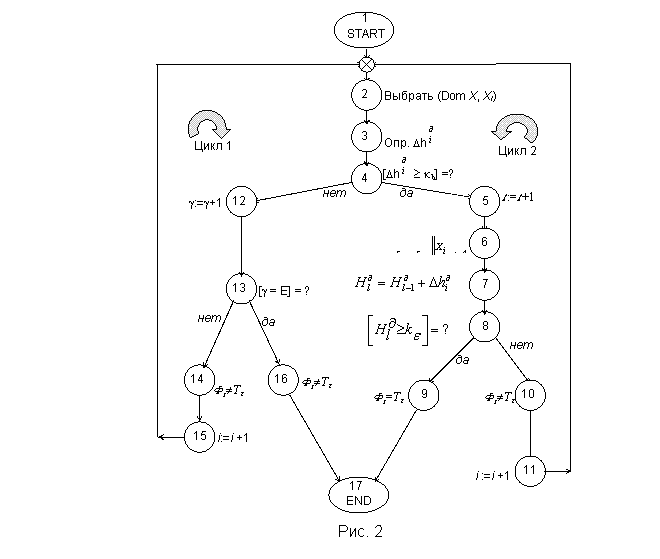
С учётом того, что тексты толерантных алгоритмов построения тестов отличаются друг от друга только в одном операторе, достаточно привести граф передачи управления (или блок-схему) только одного алгоритма (см. рис. 2) и сказать о тех операторах, которые являются различными. В данном случае таким оператором является оператор, соответствующий вершине 3 графа на рис. 2. Этот оператор определяет приращение Dh диагностической характеристики. Для цифровых устройств Dhопределяется с помощью программы моделирования неисправностей в цифровом устройстве. Для программ такой программой будет программа интерпретации или трассировки пути передачи управления. Для аналоговых устройств оператору 3 соответствует программа аналогового моделирования устройства с неисправностями. Заметим также, что критерии k_e качества диагностирования для трёх рассматриваемых классов объектов диагностирования являются качественно различными, но количественно они представляют собой некоторое натуральное число более 1. Толерантность рассматриваемых алгоритмов может быть также продемонстрирована, если записать данный алгоритм на языке T-тран [2]. Заметим также, что в основе внешнего формального сходства рассмотренных алгоритмов, отражаемого толерантным изоморфизмом, лежит некоторая внутренняя сущность, выражаемая общим законом выбора тестов, сформулированным в [2].

В заключение следует сказать, что практическая значимость понятия толерантного изоморфизма и связанного с ним толерантного вывода заключается в возможности его применения к любым сходным и постепенно развивающимся объектам, начиная от таких объектов как траектории планет, блок-схемы сходных алгоритмов [2] и кончая сходными структурами кристаллов и молекул ¾ см. примеры, приведённые выше. Таким образом, в некоторых случаях толерантный изоморфизм и соответству-ющий вывод могут служить основой для получения новых результатов в небесной механике, в теории алгоритмов, в кристаллографии и молекулярной биологии, в частности, в генетике, определённым образом дополняя теорию подобия, которая получила достаточно широкое применение в различных областях естественнонаучного знания.

Литература

1. Гольдин В. В., Журавский В. Г., Правильщиков П.А. CALS-технологии и толерантные трансляторы // Автоматика и телемеханика, 2007, № 4. Стр. 150-170.

2. Правильщиков П.А. Элементы диагностической теории толерантности и подобия. // Автоматика и телемеханика, 1992, № 10. Стр. 141-169.

3. Правильщиков П.А. Построение тестов для программ. // Автоматика и телемеханика, 1977, № 5, стр. 147-169.