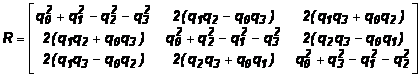Разработка методов построения полных трехмерных моделей для CAD/CAM систем по данным бесконтактных измерений

В.А. Князь,
нач. сектора,
А.Г.Позин
инж.,
ФГУП «ГосНИИАС», г. Москва

Введение

Эффективным средством подготовки геометрических данных о поверхности деталей стали бесконтактные системы измерений, позволяющие оперативно получать массивы трехмерных координат поверхности объекта с высокой точностью. Однако получаемые массивы данных («облака точек») содержат точки поверхности, видимые с заданной точки наблюдения, и для деталей сложной пространственной формы не описывают всю поверхность. Поэтому, в таких случаях необходимо производить насколько «сканов» поверхности с различных ракурсов, а затем приводить полученные фрагменты модели в единую систему координат для создания полной трехмерной модели, пригодной для дальнейшей обработки с CAD системе.

1. Методы приведения «сканов» в единую систему координат

Существует несколько подходов к получению полных трехмерных моделей для объектов сложной формы. Первый подход – создание системы многих камер, сориентированных так, чтобы каждая значимая точка объекта была видима как минимум двумя камерами. Тогда вся поверхность объекта может быть восстановлена путем совместной обработки множества изображений. Данный подход является весьма дорогим как с точки зрения стоимости необходимого аппаратного обеспечения, так и с точки зрения времени, необходимого на построение фотограмметрической сети и обработку данных съемки. Кроме того, такая многокамерная система требует перестроения ее конфигурации для каждого объекта новой формы.

Второй подход предполагает использование в системе некоторого устройства позиционирования сканируемого объекта, которое с необходимой точностью перемещает и поворачивает объект в рабочей области сканирующей системы, так что матрица перехода из локальной системы координат фрагмента объекта в глобальную систему координат полной модели определена заданными перемещениями и углами поворотами устройства позиционирования. Данный подход имеет преимущество с точки зрения обеспечения высокой степени автоматизации, но требует использования дорогостоящего высокоточного устройства позиционирования объекта.

Третий подход предполагает съемку фрагментов («сканов») модели независимо с последующим приведением их в единую глобальную систему координат с использованием только программного обеспечения. В данном подходе развиты методы построения единой модели по сети опорных точек [1], по набору соответственных точек фрагментов [2].

Однако точечные методы сопоставления требует ручной работы оператора сначала по созданию сети опорных точек на объекте, а потом по маркировке данных точек на изображениях или на трехмерной модели. Поэтому перспективными являются методы, позволяющие автоматически определять наилучшее сопоставление фрагментов по их перекрывающимся частям. Данные методы требуют, чтобы фрагменты были 3D информативны (то есть имели характерные участки рельефа для сопоставления). Ниже приведены алгоритмы, разработанные для решения задачи приведения фрагментов в единую систему координат на основе анализа перекрывающихся участков, использующиеся для подготовки данных для CAD/CAM систем

2. Описание итеративных алгоритмов

Исходные данные – фрагмент P, фрагмент X.

Задача – получить наилучшую трансформацию, приводящую фрагмент P к фрагменту X. Общий алгоритм сшивки двух фрагментов выглядит следующим образом:

1. Для текущего положения P относительно X найти пары ближайших точек {p_i,x_i}

2. В соответствии с выбранной метрикой получить трансформацию, уменьшающую расстояние (невязку) между парами {pi,xi}.

3. Применить эту трансформацию к фрагменту P.

4. Повторять пункты 1-3 до тех пор, пока уменьшение невязки не станет меньше некоторого порога.

5. Считать конечное положение фрагмента P за решение задачи.

3.1. Поиск пар ближайших точек.

Пусть P – исходные данные (подшиваемый фрагмент), X – модель, к которой подшивается P. N_p – количество точек в исходных данных, N_x – количество точек в модели. Пусть для каждой точки из P требуется найти ближайшую к ней точку из X. В простейшей реализации полного перебора она потребует O(N_pN_x) операций, или O(N²) если N≈N_p≈N_x. Для того чтобы задача была менее вычислительно сложной можно применить древовидную структуру поиска, что приводит к оценке трудоёмкости O(N_plogN_x). Преимущества такого подхода особенно заметны при работе с большими фрагментами (десятки и сотни тысяч точек в модели), выигрыш в скорости при этом составляет несколько порядков.

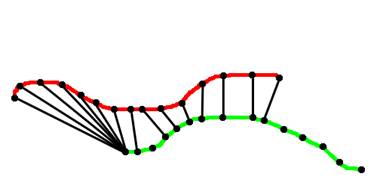
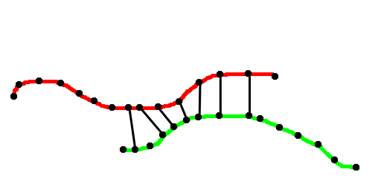
Рис 1. Слева – все пары ближайших точек для красного фрагмента. Справа – пары ближайших точек из области перекрытия

На практике редко возникает задача сшивки фрагментов одной и той же области, обычно возникает задача сшивки двух фрагментов имеющих некоторую область перекрытия. В этом случае необходимо брать только пары точек лежащих в этой области перекрытия. Пары не лежащие в области перекрытия содержат информацию, мешающую корректной работе алгоритма, и обычно приводят к неудовлетворительному общему результату. Для установления факта принадлежности пары точек области перекрытия можно из всего множества пар ближайших точек отбросить пары, одна из точек которых лежит на границе фрагмента. Оставшиеся пары считаются лежащими в зоне перекрытия фрагментов (смотри рисунок).

3.2. Метрика точка-точка

Первоначальный алгоритм итеративного сопоставления - ICP (Iterative Closest Points) был предложен Paul J. Besl и Neil D. McKay в 1992 году [3]. В нём используется метрика точка-точка. Алгоритм позволяет работать со многими представлениями фрагментов, однако внутренняя его часть всё равно работает с представлением объектов в виде точек. Метрикой расстояния d между отдельной точкой из P и моделью X будет

(1)

Пусть - ближайшая к точка из Х, то есть , где . Пусть Y – множество образовавшихся пар ближайших точек. Если C – оператор формирования ближайших точек, то Y = C(P,X). Далее, зная Y, методом наименьших квадратов вычисляются параметры вращения и перемещения для P:

,где (2)

- 7-ми мерный вектор параметров трансформации состоящий из единичного кватерниона задающего вращение - и вектора перемещения

Для получения матрицы вращения из кватерниона можно воспользоваться формулой:

(3)

3.3. Алгоритм поиска решения методом наименьших квадратов

Пусть - набор точек из исходных данных соответствующие точкам модели, причём N_x = N_p и каждая точка соответствует точке с тем же индексом. Минимизируемая функция записывается в виде

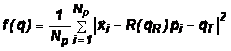(4)

Центры масс множества точек P и множества точек X вычисляются как

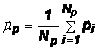и (5)

Кроссковариационная матрица множеств P и X определяется как

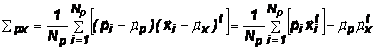(6)

Циклические компоненты антисимметричной матрицы используются для формирования вектора-столбца . Этот вектор затем используется для формирования симметричной 4x4 матрицы :

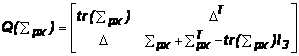, где (7)

I₃ – единичная матрица 3x3.

Единичный собственный вектор соответствующий максимальному собственному значению матрицы выбирается в качестве кватерниона оптимального поворота. Вектор оптимального переноса вычисляется как

(8)

Операция поиска решения методом наименьших квадратов обозначается как

, где (9)

d_ms – метрика расстояния между точками.

3.4 Метрика точка-плоскость

Метрика точка-плоскость известна как метрика Y.Chen и G.Medioni и используется во многих работах, например в [4].

Пусть P и X – два фрагмента, или два набора точек с нормалями. Эти нормали могут быть получены из внешних источников или рассчитаны усреднением нормалей прилегающих треугольников. Для каждой точки из P выбирается ближайшая из X, таким образом, формируется N пар точек {p_i,x_i}, причём каждая x_i содержит нормаль n_i. Мы пытаемся найти трансформацию, состоящую из вращения R и переноса t, минимизирующую сумму квадратов расстояний от каждой точки p_i до плоскости перпендикулярной X в точке x_i. Ошибка выравнивания задаётся формулой:

(10)

Если считать повороты небольшими, приведённое уравнение может быть решено через линеаризацию матрицы вращения R. В этом случае трансформация эквивалентна смещению на вектор , где - 3x1 вектор вращения вокруг осей x,y,z, и - вектор параллельного переноса. Переписывая уравнение и раскрывая скобки, получаем, что мы ищем 6-ти мерный вектор минимизирующий функцию:

(11)

Параметры трансформации можно найти, продифференцировав полученное уравнение по r и t. Таким образом, получается линейная система Cy = b, где y – вектор 6x1 состоящий из параметров трансформации, C – ковариационная матрица 6x6:

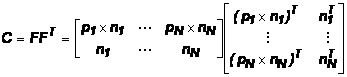(12)

3.5 Сравнение метрик точка-точка и точка-плоскость

Метрику точка-точка можно представить как набор пружин связывающих пары точек. Конечное положение ищется методом наименьших квадратов. При этом устойчивость решения не зависит от начального расположения точек.

Метрику точка-плоскость тоже можно представить в виде набора пружин. Один конец пружины связан с первой точкой пары, другой может свободно скользить по плоскости проходящей через вторую точку пары и перпендикулярной её нормали. Метод выравнивания с использованием метрики точка-плоскость опирается на предположение, что последовательные уточнения положения получаются с использованием поворотов только на небольшие углы, поэтому первоначальное положение точек не должно сильно отличаться от их конечного положения.

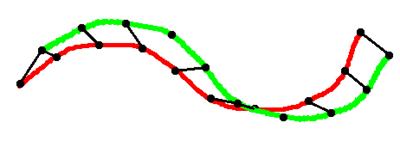
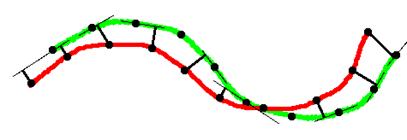
Рис 2. Слева – “пружинки” для метрики точка-точка. Справа – “пружинки” для метрики точка-плоскость

Для задачи сшивки двух отсканированных фрагментов рекомендуется использовать метрику точка-плоскость. В пользу этого говорят несколько фактов:

- Метрика точка-плоскость обеспечивает сходимость за меньшее количество итераций.

- В метрике точка-плоскость ошибка в выборе парной точки не оказывает существенного воздействия на конечный результат, если нормаль выбранной точки отличается от нормали действительно парной точки незначительно. В то же время ошибка в выборе парной точки для метрики точка-точка мешает алгоритму найти верное положение фрагмента.

- Для достижения высокой точности сшивки при использовании метрики точка-точка требуется большее количество пар, чем при использовании метрики точка-плоскость. Это связано с тем, что метрика точка-точка использует дискретное представление поверхности, в то время как метрика точка-плоскость использует линейную интерполяцию.

На нижеприведённых рисунках показано первоначальное положение двух фрагментов полученное в 3D редакторе и результаты сшивки, полученные при помощи метрики точка-точка (слева) и точка-плоскость (справа). Очевидно, что качество сопоставления в случае использования метрики точка-плоскость значительно выше по сравнению с использованием метрики точка-точка.

Рис 3. Два совмещённых фрагмента. Слева – совмещено оператором в 3D редакторе. В центре - с использованием метрики точка-точка. Справа - с использованием метрики точка-плоскость

Заключение

В работе описаны методы, используемые при создании полных трехмерных моделей объектов сложной формы по данным бесконтактных трехмерных измерений. Они хорошо зарекомендовали себя в практике построения единых моделей для CAD/CAM приложений. Дальнейшими направлениями развития данной технологии являются одновременная сшивка группы фрагментов [5], получение единой сетки всей модели [6] и наложение качественной цветной текстуры [7].

Литература

1. Knyaz V.A., Stepanyantc D.G., PC-Based Digital Close-Range Photogrammetric System for Rapid 3D Data Input in Cad Systems, International Archives of Photogrammetry and Remote Sensing, Vol. XXXIII, part B5/2, Amsterdam, The Netherlands, 2000, pp. 756-763

2. Князь В.А., Амелин В.В. Объединение фрагментов трехмерной модели объекта. Материалы 12 Международной Конференции по Компьютерной Графике и Машинному Зрению Графикон’2002, Нижний Новгород, 16-21 сентября 2002 г., стр. 99-103

3. Paul J. Besl and Neil D. McKay “A Method for Registration of 3-D Shapes.”

4. Natasha Gelfand, Leslie Ikemoto, Szymon Rusinkiewicz, Marc Levoy “Geometrically Stable Sampling for the ICP Algorithm.”

5. Kari Pulli “Multiview Registration for Large Data Sets.”

6. Brian Curless and Marc Levoy “A Volumetric Method for Building Complex Models from Range Images.”

7. Fausto Bernardini, Ioanna M.Martin, Holly Rushmeier “High-Quality Texture Reconstruction from Multiple Scans.”